3Blue1Brown_线代本质第一章：向量究竟是什么

• 我开始了3蓝1棕的线性代数本质的学习，我没什么基础所以在此做了笔记，学习永远不怕晚哈！如有问题请各位大佬及时指正！
• 在b站它的链接在此。
• 官方一共将此系列分为12节，所以我也会分开写。
• 我会把相关的这一系列笔记链接在每一篇的最下面，写完就会更新，有需要的朋友可以自行跳转！
• 这就是普通的记录，比较基础，没什么有新意的地方。厉害的大佬或相关专业的大佬可以自行跳过此笔记！

---

✏️向量基本解释：

• 在线性代数中，最基础，最根源的组成部分就是向量
• 一般来说，有三种看待向量的观点，他们看似不同却有所关联。
  • 物理专业的角度
  • 数学角度
  • 计算机角度

---

📝物理专业的角度：

• 向量是空间中的箭头。
• 决定一个向量的是：
  1. 它的长度。
  2. 它所指的方向。
• 只要上述两个特征不改变，就可以自由移动一个向量而保持它本身不被改变。
• 处在平面中的向量是二维的。
• 处在生活空间中的向量是三维的。

---

📝计算机角度：

• 向量是有序的数字列表。
• 比如你正在做一个有关房价的分析，你关心的只有两个特征：
  1. 房屋面积。
  2. 房屋价格。
• 注意数字列表的数字顺序不可颠倒
• 在这个房屋的例子里可以表述为：用二维向量对房屋进行建模。
• 在这里，向量只不过是列表的一个花哨的说法，这个向量是二维的因为它的列表长度是2。

---

📝数学角度：

• 向量可以是任何东西，只要保证两个向量相加以及数字与向量相乘是有意义的即可。
• 这种方式看待向量就较为抽象了。这里可以看出，向量加法和向量数乘贯穿线性代数，二者起着很重要的作用。

---

✏️向量思考方式：

• 首先考虑一个坐落在某个坐标系（例如x-y平面）中的箭头，箭头起点位于原点。
• 在线性代数中，向量经常以原点作为起点；这与物理学理念（向量可以在空间中自由落脚）不同。
• 一旦理解了【向量是空间中的箭头】，那么我们可以通过【向量坐标】来理解【向量是一个有序数字列表】
• 因为这两种观念的碰撞，恰恰形成了线性代数中的重要概念。

---

📝平面空间内：

• 来看这个箭头在x-y平面空间内（每个间距单位为1），它的这对数指导我们如何从原点（向量起点）出发到达它的尖端（向量终点）。
• 第一个数告诉我们沿着x轴走多远，正数代表向右移动，负数代表向左移动。
• 第二个数告诉我们沿着y轴走多远。正数代表向上移动，负数代表向下移动。
• 为了把向量和点区别开，向量采用的写法是将这对数竖着写，并用方括号括起来。（（-2，3）这样表示的向量也是可以的，没有区别）。
• 每一对数给出为一一个向量（有且只有一个）。
• 每一个向量恰好对应为一一对数。

---

📝三维空间内：

• 三维空间内我们再添加一个垂直于x轴和y轴的第三根z轴
• 这种情况下，每个向量就与一个有序的三元数组对应。
• 第一个数告诉你沿平行x轴走多远，第二个数告诉你沿平行y轴走多远，第三个数告诉你沿平行z轴走多远。
• 每个三元数组给出为一一个向量。
• 每个向量对应唯一的三元数组。

---

📝向量加法和向量数乘：

• 线性代数中每一个主题都围绕着这两种运算。

✍️向量加法：

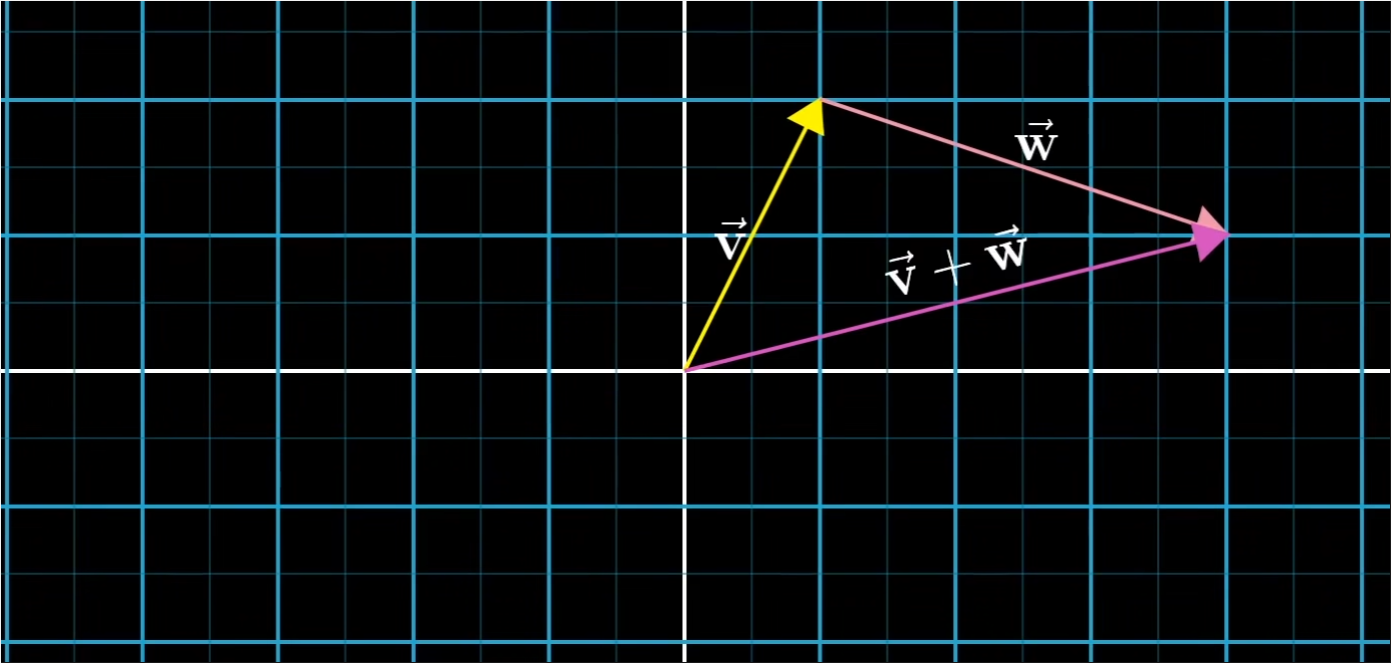
• 向量加法：
  • 我们通过平移第二个向量，使他的起点与第一个向量的终点重合；然后画一个向量，它从第一个向量的起点出发，指向第二个向量的终点；这个向量就是他们的和
• 向量加法的定义差不多是线代中唯一允许向量离开原点的情形。
• 我们可以把向量加法看作数轴上加法的一种扩展。
  
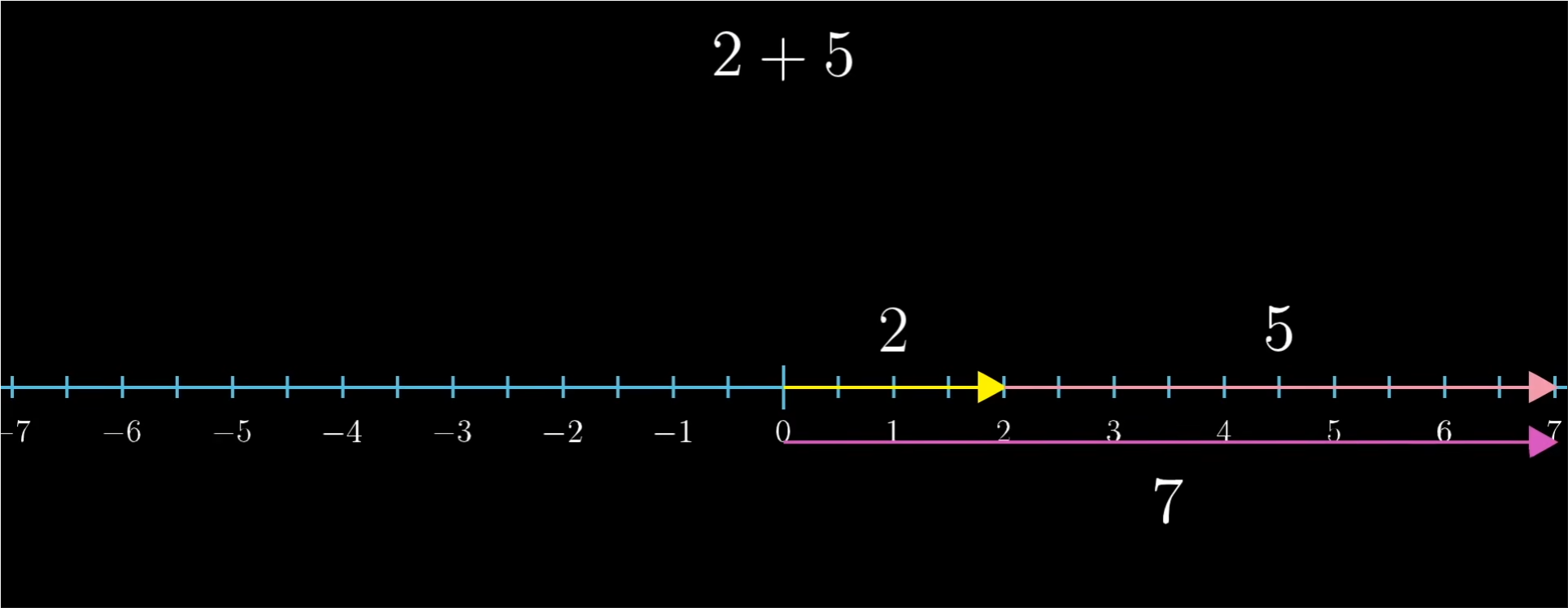
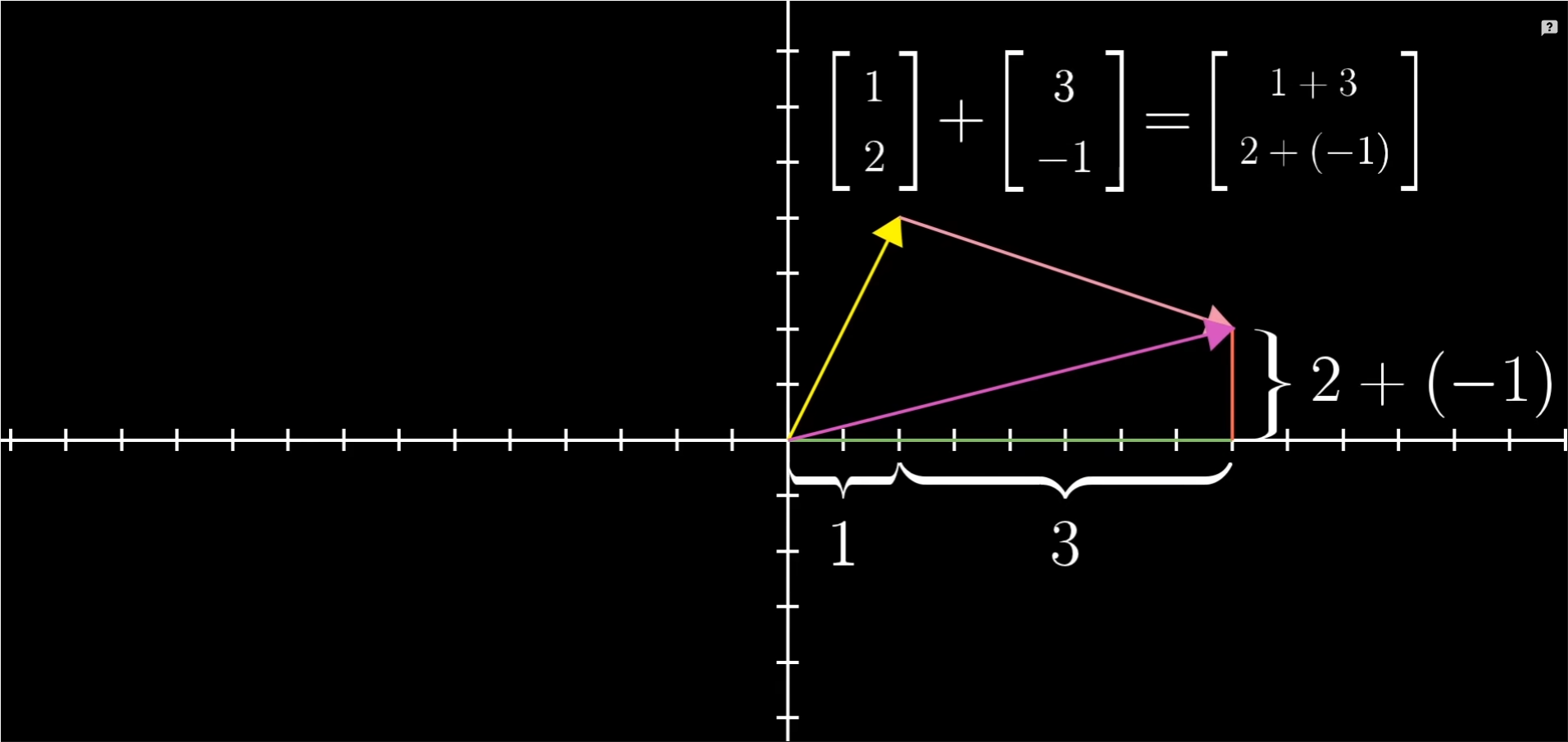
• 回到x-y平面内，我们可以以下图方式所思考向量的加法，即：它朝着x轴，y轴分别运动的总量；先完成它水平运动，再完成竖直运动。
  

---

✍️向量数乘：

• 向量与其他数（标量）相乘的方式叫做“Scaling”（缩放）。
• 数字（标量）在线性代数的作用就是缩放向量；负数与向量相乘则会改变向量的方向。

---

📝总结：

• 怎么看待向量都无所谓，它的实际作用也很少体现在这些观点的其中一个上，而是更多的体现在它能够在这些观点中相互转化。
• 线性代数为数据分析提供了一条将大量数据列表概念化，可视化的渠道。他让数据样式变得非常明晰，并让我们了解特定运算的意义。
• 另一方面，线代给物理学家和计算机图形程序员提供了一种语言，让他们通过计算机能处理的数字来描述并操纵空间。

---