3Blue1Brown_线代本质第二章：线性组合，张成的空间与基

  • 我开始了3蓝1棕的线性代数本质的学习，我没什么基础所以在此做了笔记，这里是第二章打卡，学习永远不怕晚哈！如有问题请各位大佬及时指正！
  • 在b站它的链接在此。
  • 官方一共将此系列分为12节，所以我也会分开写。
  • 我会把相关的这一系列笔记链接在每一篇的最下面，写完就会更新，有需要的朋友可以自行跳转！
  • 这就是普通的记录，比较基础，没什么有新意的地方。厉害的大佬或相关专业的大佬可以自行跳过此笔记！

✏️基向量：

✍️在xy坐标系中两个特殊向量：

  • 一个指向正右方，长度为1，通常被称为“i-hat”（i帽）或x方向的单位向量。
  • 另一个指向正上方，长度为1，通常被称为“j-hat”（j帽）或者y方向的单位向量。
  • i-hat与j-hat这两个向量有特殊的名称，他们是xy坐标轴的“基向量”（basis vector）。
  • 这是在表述：当你把坐标看为标量时，基向量实际上就是这些标量的缩放对象。

✍️例子1：

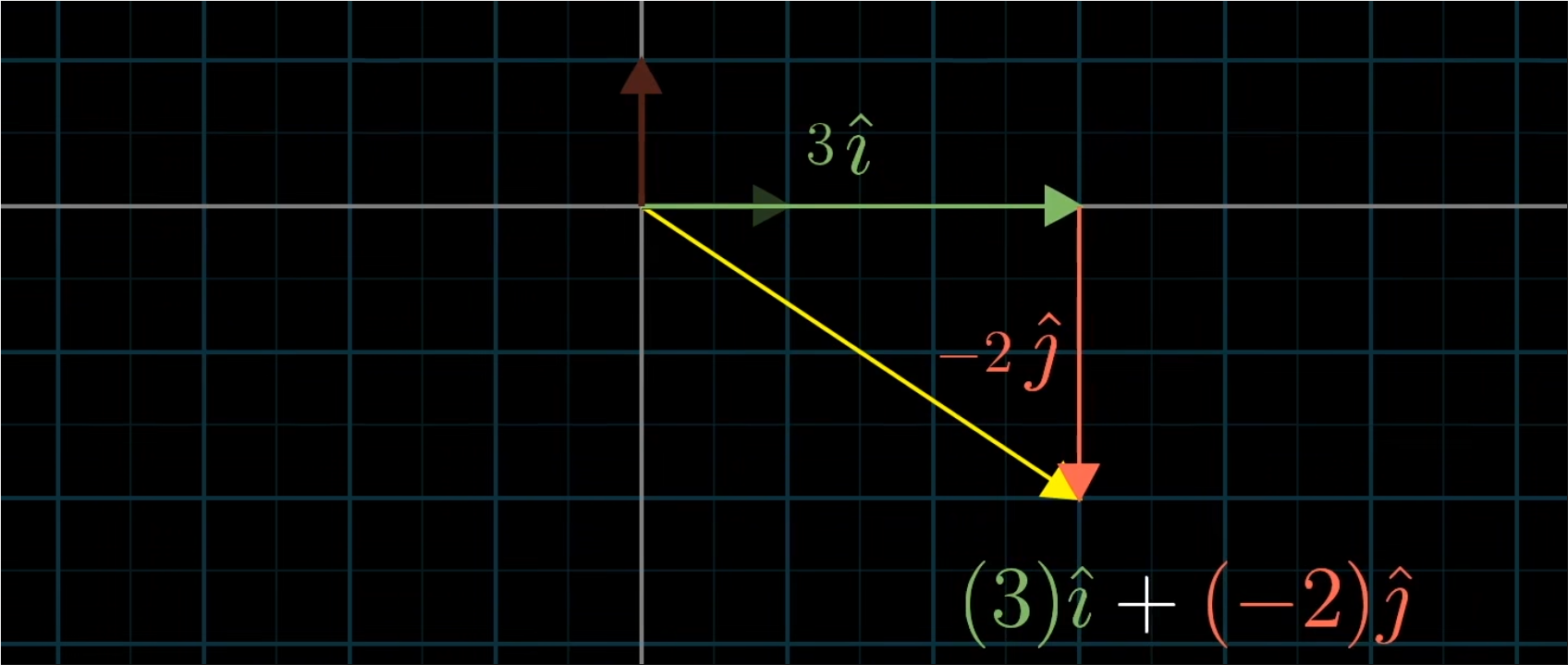
ihat_jhat

  • 由上图示意看出，（3，-2）可以想象为：x坐标是一个标量，它将i帽拉升为原来的三倍；y坐标也是一个标量，它将j帽反向并拉伸为原来的两倍。从这个角度看，这个向量实际上是两个经过缩放的向量的和。
  • “缩放向量并且相加”这一概念十分重要。

✍️如果我们选择不同的基向量会怎么样：

  • 我们完全可以选择不同的基向量，获得一个合理的新坐标系。
  • 比如随便选一个指向右上方的向量，再随便选择一个指向右下方的向量，想象通过选择两个标量，分别用于缩放二者的其中一个， 然后把他们相加，就可以得到不同的结果。通过改变所选择的向量，我们可以得到所有向量。
  • 一对新的基向量，同样允许我们在一对数和二维向量之间自由转化。但是这种变化关系与我们之前使用的i帽和j帽的变化关系完全不同。
  • 每当我们用数字描述向量的时候，它都依赖于我们正在使用的基。
  • 两个数乘向量的和被称为这两个向量的线性组合（Linear combination）。
  • 那么线性怎么来的可以考虑为： 如果固定其中一个标量，让另一个标量自由变化，所产生的终点会描述出一条直线，如下图所示。
    linearCombination
  • 如果让两个标量同时自由变换，考虑所有可得到的向量，可能有两种情况（实际是三种）：
    1. 大部分情况下，对于一对初始向量，你能达到平面中每一个点；所有二维向量都尽在掌握。
    2. 另一种较为糟糕的情况是，当两个初始向量恰好共线时，所产生的向量的终点被限制在一条过原点的直线上。
    3. 事实上还有第三种情况就是，两个向量都是零向量,那就只能在原点了。
      向量变换的三种情况

✏️张成空间（span）：

概念：
- 所有可以表示为给定向量线性组合的向量的集合，被成为给定向量张成的空间。

  • 下图：向量全部线性组合构成的向量集合成为“张成的空间”，a与b在实数范围内变动。
  • 张成空间

✍️二维空间内张成空间：

  • 通常情况下，我们用向量的终点代表向量（起点是原点）；用这种方法来看，如果要考虑落在一条直线上所有向量的时候，只需要考虑直线本身就行了。所以也可以考虑为，如果同时考虑xy坐标系中所有向量，将每个向量抽象为它的终点，实际上就不用考虑所有的肩头了，只需要考虑无限大的二维平面本身即可。
  • 如果考虑一个向量，我们就可以把他看作箭头；如果考虑多个向量，则可以把他们都看作是点。
  • 对大部分二维向量来说，它们的张成空间是整个无限大的二维平面；但如果共线，他们的张成空间就是一条直线。

✍️三维空间内张成空间：

在三维空间中取两个指向不同方向的向量，他们的张成空间是这样的：

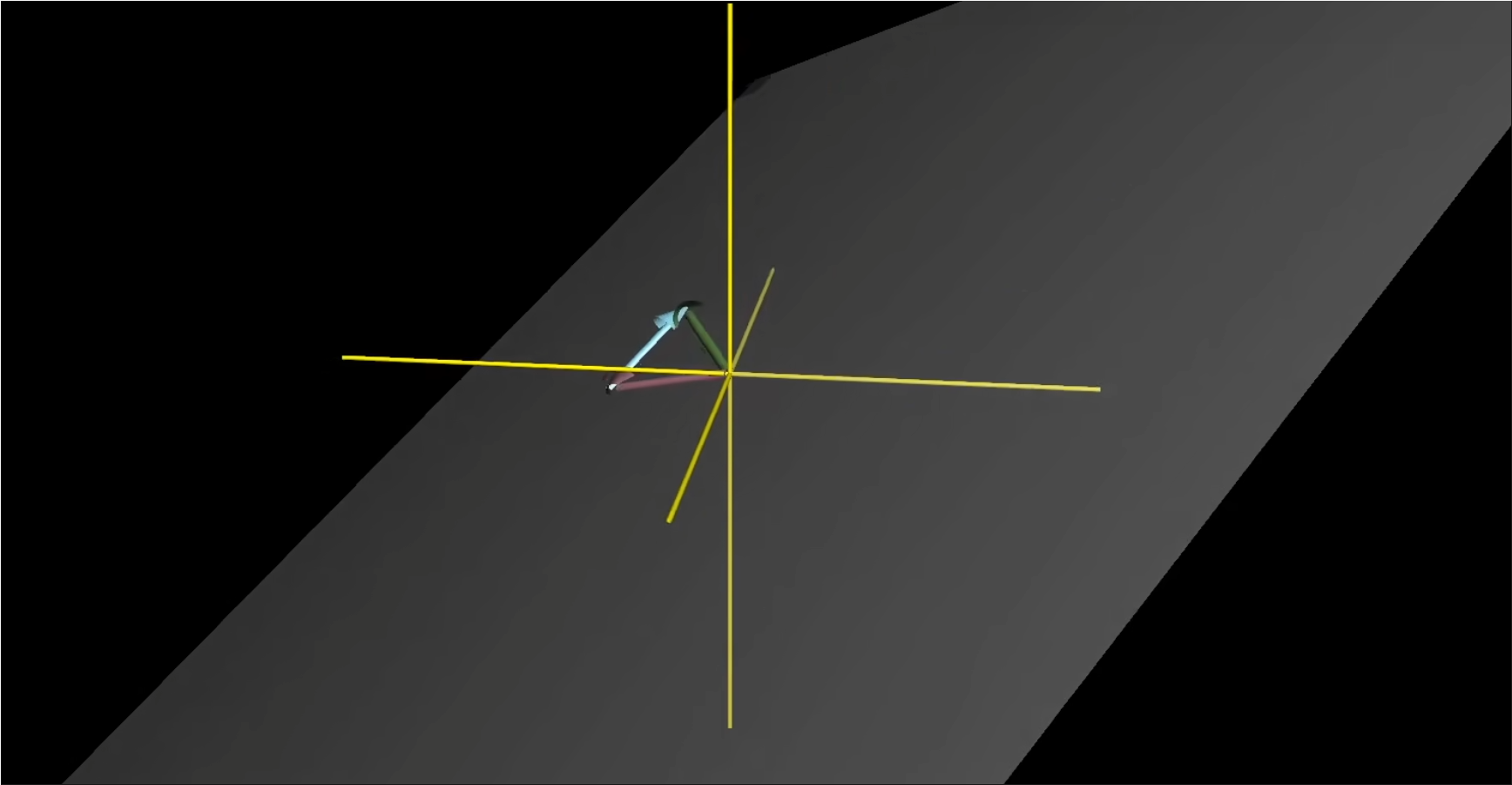
两个向量在三维空间

  • 这两个向量的张成空间就是他们所有可能的线性组合；也就是缩放再相加之后所有可得到的向量。
  • 逐渐改变线性组合中的这两个标量，把缩放后的向量相加，然后跟着最终向量的终点走，这个终点会画出三维空间中某个过原点的平面；这个平面就是这两个向量的张成空间。（所有终点落在这个平面上的向量集合是这两个向量的张成空间）

如果加上第三个向量，他们的张成空间是这样的：

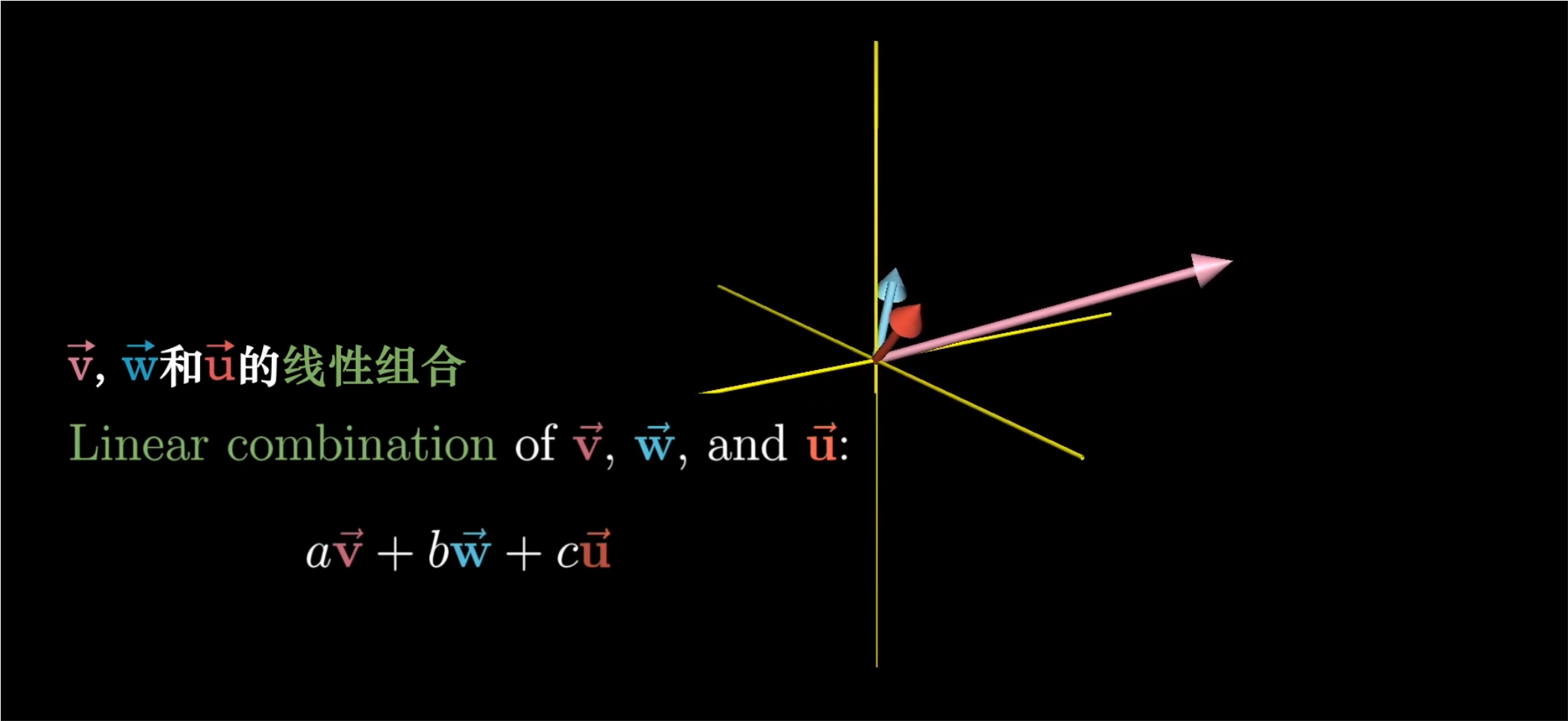
三个向量在三维空间

  • 选择三个向量分别进行缩放，然后把结果相加。
  • 这三个向量所有可能的线性作何构成了他们的张成空间。
  • 如果第三个向量恰好落在前两个向量所张成的平面上，那么他们张成的空间并不改变，还是在这个平面中。
  • 但是如果随机选一个向量，他几乎不可能落在前两个向量所张成的平面中；这种情况下，由于第三个向量指向不同的方向，我们就能得到所有的三维向量。（可以考虑成：当我们缩放第三个向量的时候，他将前两个向量张成平面来回沿着它的方向移动，从而扫过整个三维空间。）

✏️Linearly dependent 和 Linearly Independent：

当向量共线的情况，或第三个向量恰好落在之前向量生成的平面的情况下：

  • 这种情况说明一组向量中至少有一个是多余的，没有对张成空间做出任何贡献，我们取走这个多余的向量也不减少张成空间，这样的情况下，我们称它为“线性相关”（Linearly dependent）的。

如果所有向量都给张成空间添加了新的维度：

  • 这种情况就称之为“线性无关”（Linearly Independent）的。

✏️基的严格定义（Technical definition of basis）：

  • The basis of a vector space is a set of linearly independent vectors that span the full space
    (向量空间的一组基是张成该空间的一个线性无关向量集)
    基的严格定义