3Blue1Brown_线代本质第三章：矩阵与线性变换

  • 我开始了3蓝1棕的线性代数本质的学习，我没什么基础所以在此做了笔记，这里是第三章打卡，学习永远不怕晚哈！如有问题请各位大佬及时指正！
  • 在b站它的链接在此。
  • 官方一共将此系列分为12节，所以我也会分开写。
  • 我会把相关的这一系列笔记链接在每一篇的最下面，写完就会更新，有需要的朋友可以自行跳转！
  • 这就是普通的记录，比较基础，没什么有新意的地方。厉害的大佬或相关专业的大佬可以自行跳过此笔记！

✏️线性变换：

【注：这章节讨论在二维空间的样子，以及与矩阵向量乘法的关联，并展示一种不用死记硬背的考虑矩阵向量乘法的方法。】

✍️解析“线性变换”：

  • Linear Transformation = Linear Function
  • “变换”（Transformation）本质上是“函数”（function）的一种花哨的说法；它接受输入内容，并输出对应结果。
  • 变换和函数意义相同还要用不同的词汇表达的原因是：使用“变换”是在暗示以特定的方式来可视化这一“输入”“输出”关系；“变换”这个词在按时我们用运动去思考。
  • 每一个输入向量都移动到输出向量的位置：将向量看作是点，那么变换就是空间中的点移动到其他点的位置。
  • 直观的说，如果一个变换具有以下两条性质，我们就可以称它是线性的：
    1. 直线在变换后仍然保持为直线，不能有所弯曲。
    2. 原点保持固定。
    线性变换规则
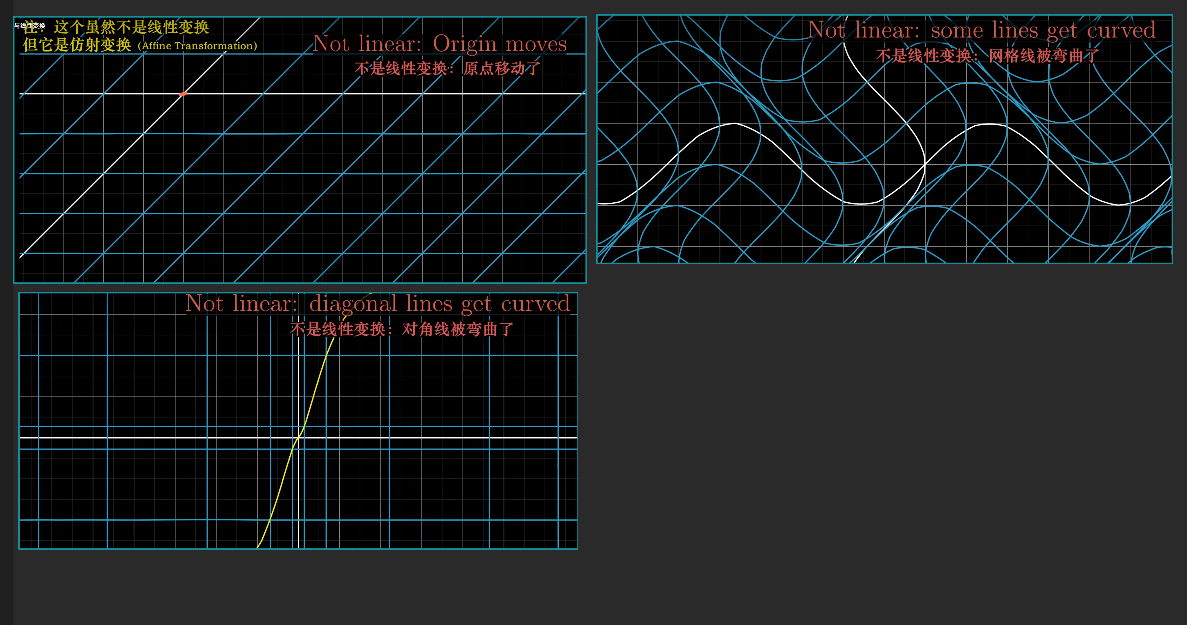
    20220924214734
  • 总的来说，可以把线性变换看作是“保持网格线平行且等距分布”的变换。部分线性变换比较容易思考，如：网格以原点为轴心进行旋转；其他的则稍加复杂。
    线性变换

✍️如何用数值描述线性变换：

  • 我们给出一个向量坐标，希望得到一个变换后向量的坐标只需要通过：

    • 记录两个基向量i帽和j帽变换后的位置，其他向量也会随之而动

  • 由下图可视，向量v的坐标原本为（-1，2），这个向量可以看作为-1与i帽之积和2与j帽之基的和。如果运用一些变换，使得向量一起运动，并尊重“网格保持平行且等距分布”这个原则，变换后的向量v的位置，就是-1与变换后i帽之积加上2与变换后j帽之积。

  • 换句话说，向量v是i帽和j帽的一个特定线性组合；那么变换后的向量v也是变换后i帽与j帽同样的线性组合。这就意味着，你可以只根据变换后的i帽与j帽，就推断出变化后的v。
    数值描述线性变换

  • 一般情况下，一个向量的坐标是（x，y），变换后的向量就是x乘变换后的i帽，加上y乘变换后的j帽。
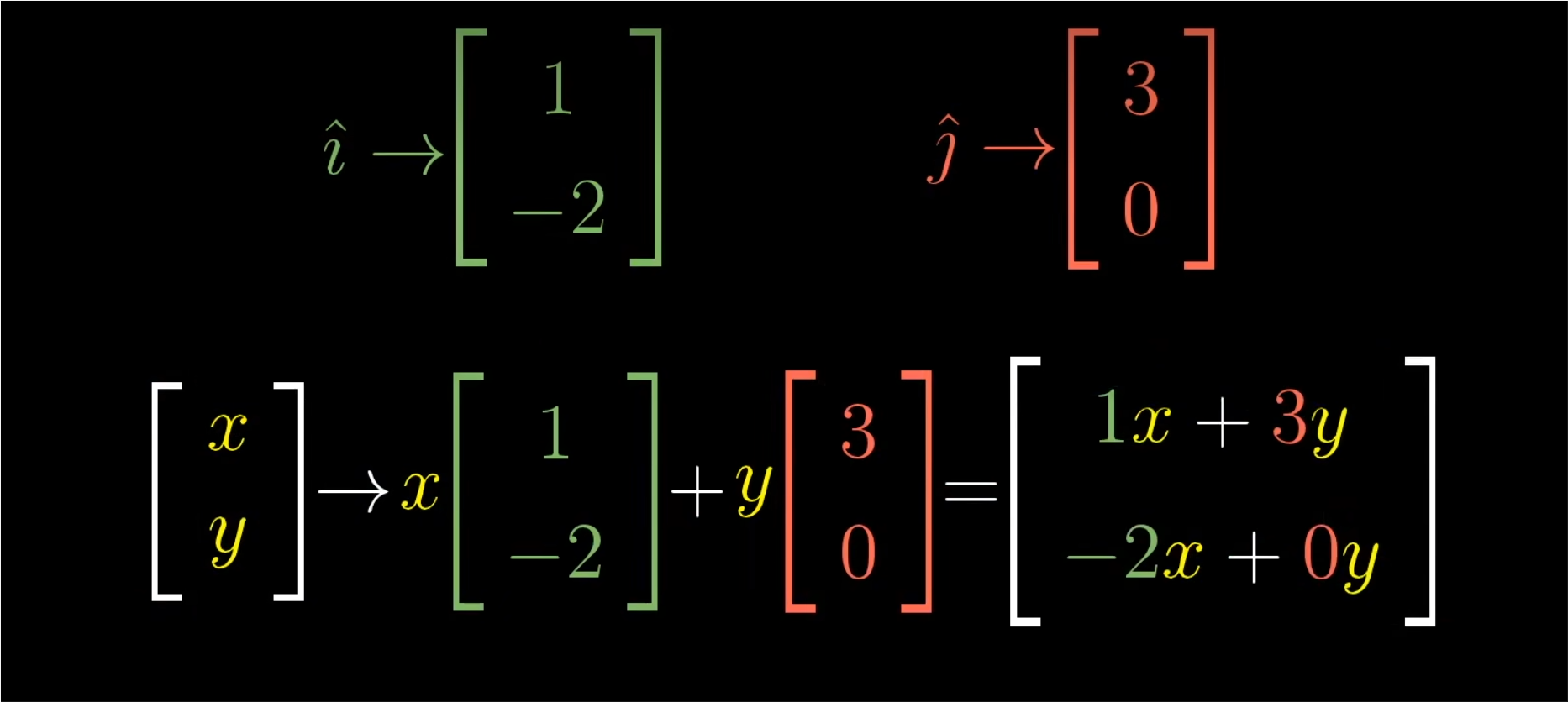
    公式png

  • 一个二维线性变换仅由四个数字完全确定：变换后i帽的两个坐标与变换后j帽的两个作坐标。

  • 通常我们将这些坐标装在一个2x2的格子中，称它为2x2矩阵。

✏️矩阵：

  • 如果有一个描述线性变换的2x2矩阵，以及一个给定的初始向量，你只需要取初始向量的坐标，将他们分别于矩阵的特定列相乘，然后结果相加即可。这与“缩放基向量再相加”的思想一致。
  • 矩阵在这里只是一个记号，它含有描述线性变换的信息。
  • 如下图所示：我们可以把矩阵的第一列（a，c）看作是变换后第一个基向量，把第二列（b，d）看作是变换后第二个基向量；我们将这个变换作用于向量（x，y），它的结果就是（ax+by，cx+dy）。我们可以把它定义为矩阵向量乘法。矩阵放在向量左边，类似一个函数。
    2x2矩阵公式
    矩阵向量乘法
  • 我们完全可以把矩阵的列看作变换后的基向量，把矩阵向量的乘法看作他们的线性组合。
  • 线性变换是操纵空间的一种手段；这种变换只需要几个数字就可以描述清楚，这些数字就是变换后的基向量的坐标。

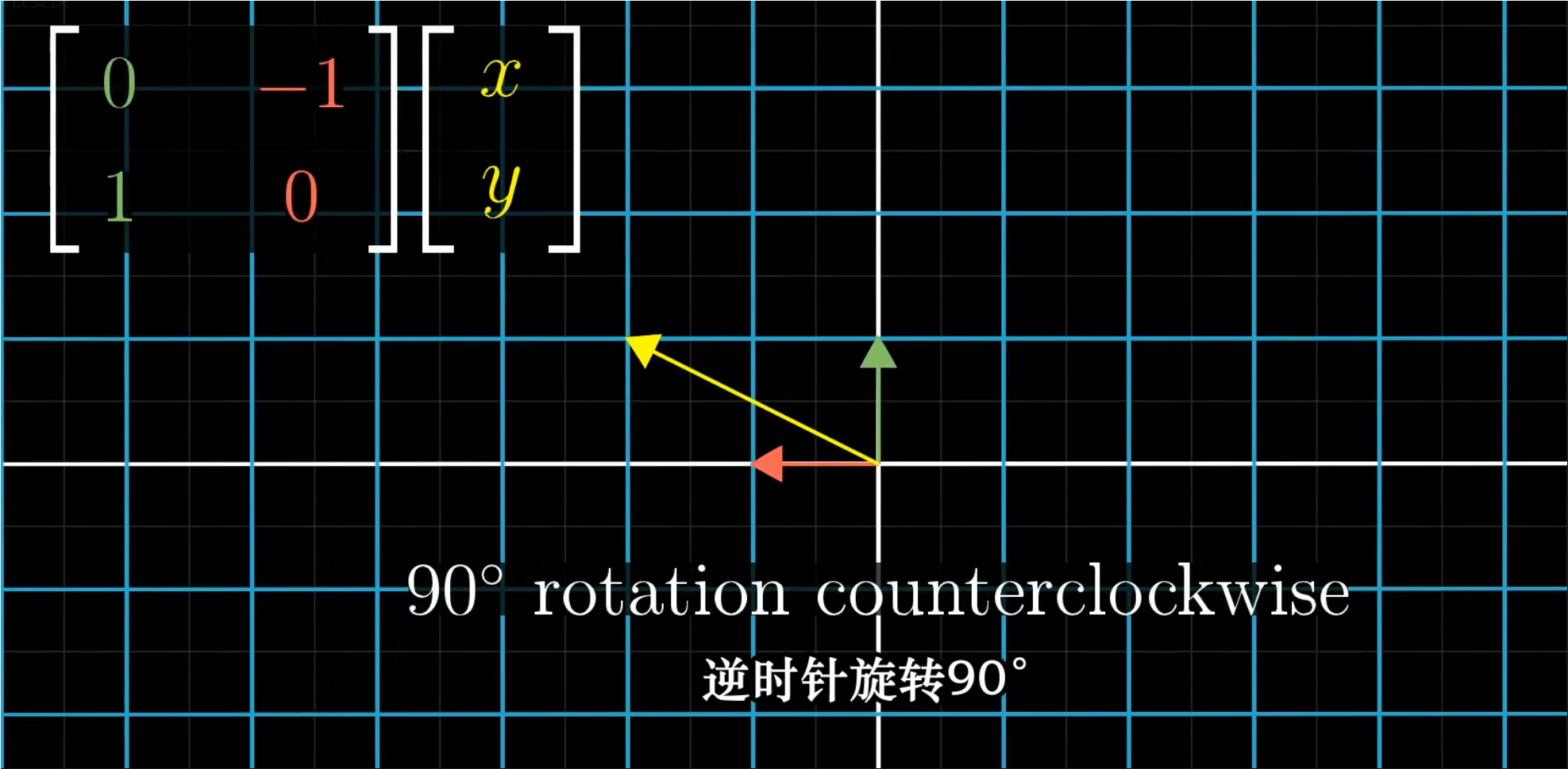
✍️示例：逆时针旋转90度

  • 如下图示例，i帽初始为（1，0），j帽初始为（0，1）；如果将他们逆时针旋转90度，那么变换后的i帽就是（0，-1），j帽就是（-1，0）。
  • 如果此时我们想计算一个向量逆时针旋转90度：可以直接将这个向量（x，y）与变换后的i帽与j帽相乘。
    向量逆时针旋转90度案例

✍️Shear（剪切/错切）：

  • i帽保持为（1，0），j帽移动到坐标（1，1）。为了计算一个向量变换后的位置，可以直接将向量与这个矩阵相乘。
    shear

✍️反向思考：

  • 如果我们希望推测一个矩阵代表的线性变换是什么样的，我们可以将i帽与j帽先移动到变换后的位置，空间其他剩余部分则跟随二者一起运动，以保持网格线平行且等距分布。
  • 如果变换后的i帽和变换后的j帽是线性相关的，意味着其中一个向量是另一个的倍数，那么这个线性变换将整个二维空间挤压到他们所在的一条直线上，也就是这儿两个线性相关向量所张成的一维空间。

✏️总结：

  • 总之，线性变换是操纵空间的一种手段，它保持网格线平行且等距分布，并且保持原点不动。
  • 这种变换只需要几个数字就能够描述清楚，这些数字就是变换后基向量的坐标；以这些坐标为列所构成的矩阵为我们提供了一种描述线性变换的语言。矩阵向量乘法就是计算线性变换作用于给定向量的一种途径。
  • 矩阵都可以理解为对空间的一种特定变换。