3Blue1Brown_线代本质第四章：矩阵乘法与线性变换复合

  • 我开始了3蓝1棕的线性代数本质的学习，我没什么基础所以在此做了笔记，这里是第四章打卡，学习永远不怕晚哈！如有问题请各位大佬及时指正！
  • 在b站它的链接在此。
  • 官方一共将此系列分为12节，所以我也会分开写。
  • 我会把相关的这一系列笔记链接在每一篇的最下面，写完就会更新，有需要的朋友可以自行跳转！
  • 这就是普通的记录，比较基础，没什么有新意的地方。厉害的大佬或相关专业的大佬可以自行跳过此笔记！

【注：本章笔记是第四章加附注一的笔记，也就是《矩阵乘法与线性变换复合》加《三维空间中的线性变换》。】

✏️线性复合变换：

  • 有时候，我们常常是想要做多种变换，比如“先旋转，后剪切”；这个新的线性变换通常被称为前两个独立变换的“复合变换”（Composition）。
  • 和其他变换一样，我们可以通过追踪i帽和j帽的变换，并用矩阵完全描述这个复合变换。
  • 两个矩阵相乘有着几何意义，也就是两个线性变换相继作用。
    复合矩阵
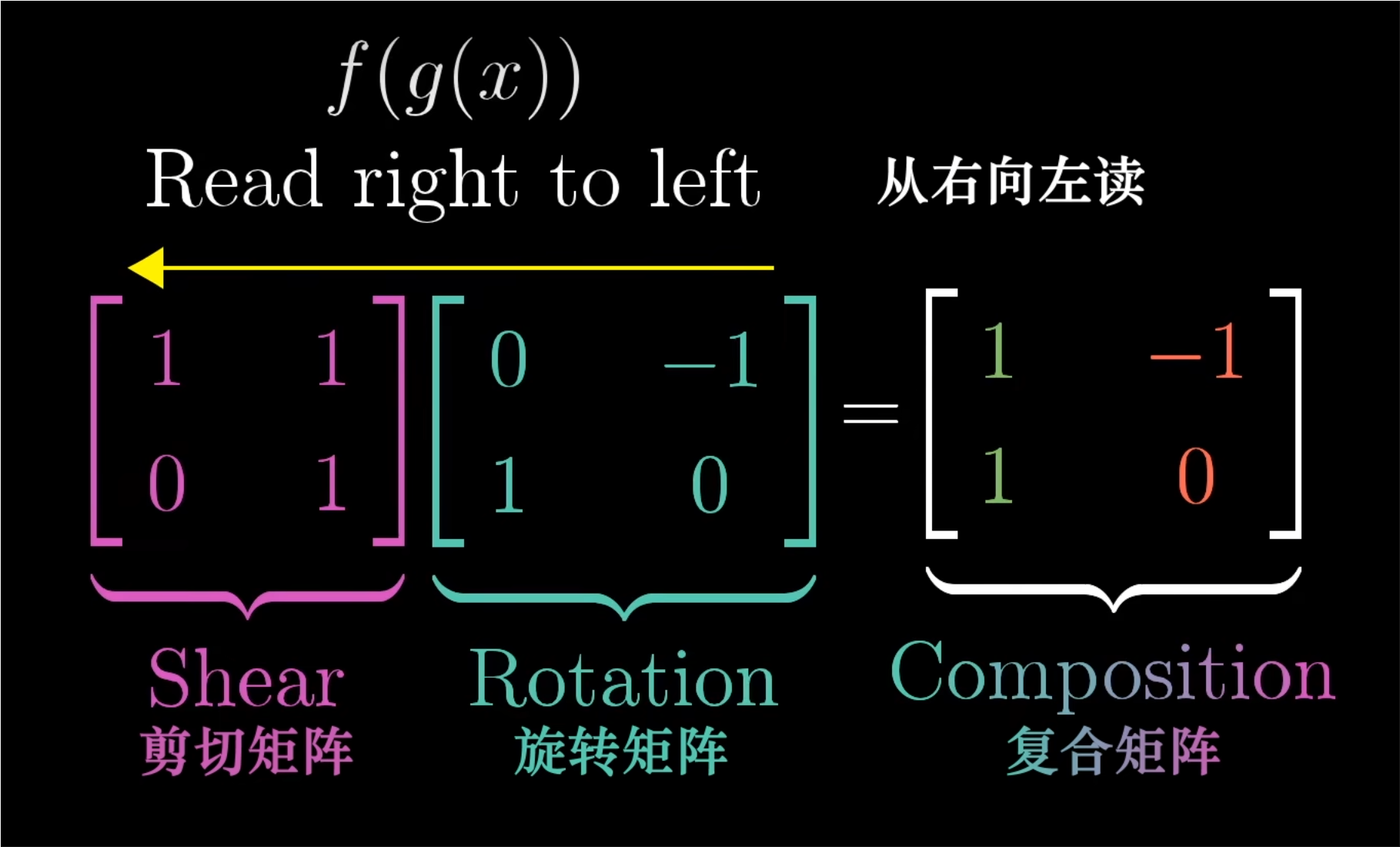
  • 这个矩阵需要从右向左读；首先应用右侧矩阵所描述的变换，然后再应用左侧矩阵所描述的变换。
  • 它起源于函数的记号，因为我们将函数写在变量左侧。所以每次将两个函数复合的时候，我们需要从右往左读。

✍️复合矩阵的计算：

  • 我们希望对复合矩阵进行计算的时候，计算结果的第一列我们首先要考虑：i帽去哪里了？
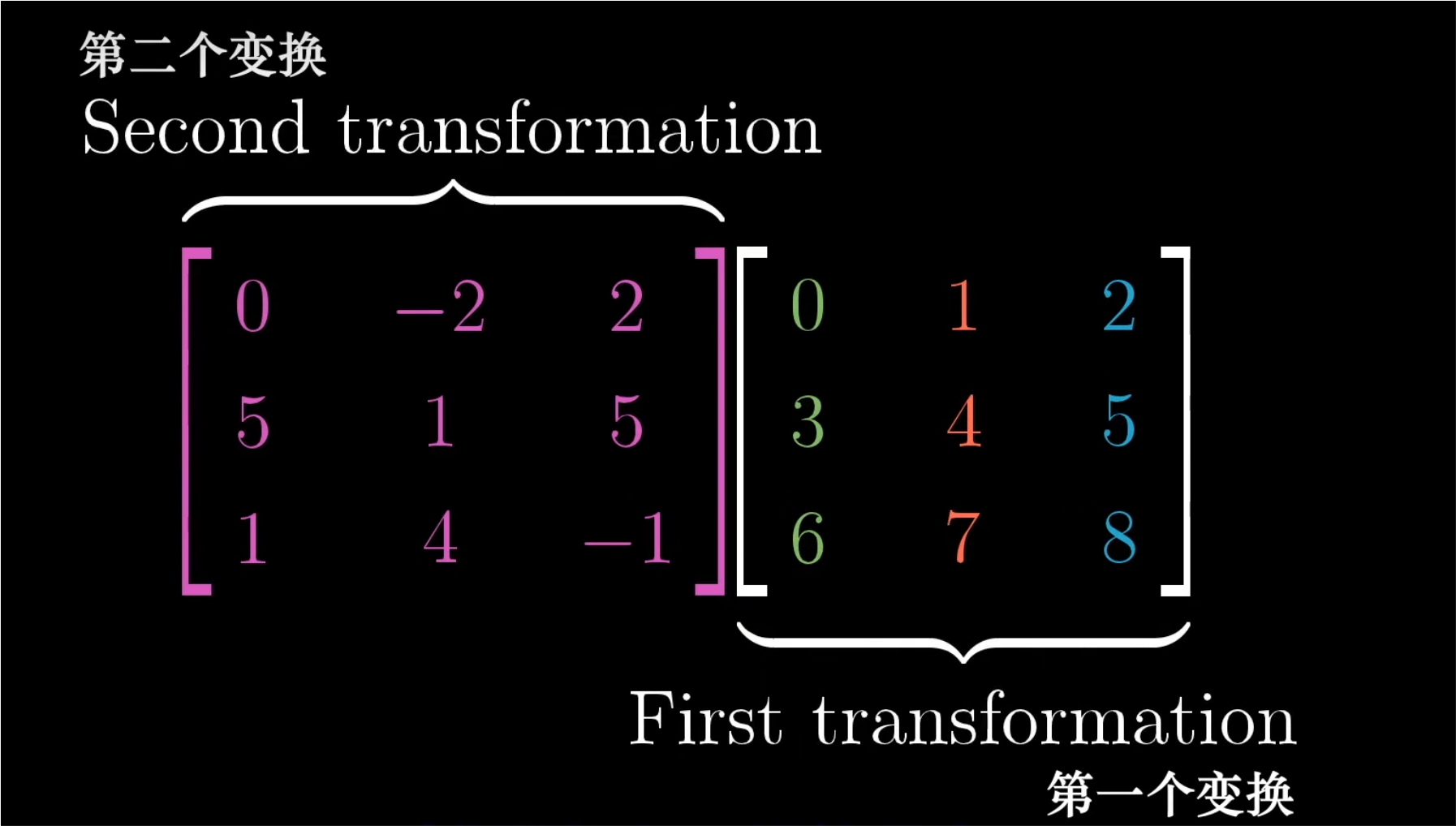
  • 下图看出，i帽首先落在（1，1）。所以我们在计算时首先将示例中的M1的第一列（1，1）拿出来，与M2进行运算，将M2的变换作用于这个向量，得到最终计算结果的第一列。
    复合矩阵示例_i帽变换
  • 其次，我们要考虑第二列：j帽去哪了？
  • 与上文中提到的i帽的计算方式一样，j帽先落在（-2，0），所以我们在计算时将示例中的M1的第一列（-2，0）拿出来，与M2进行运算，将M2的变换作用于这个向量，得到最终计算结果的第二列。
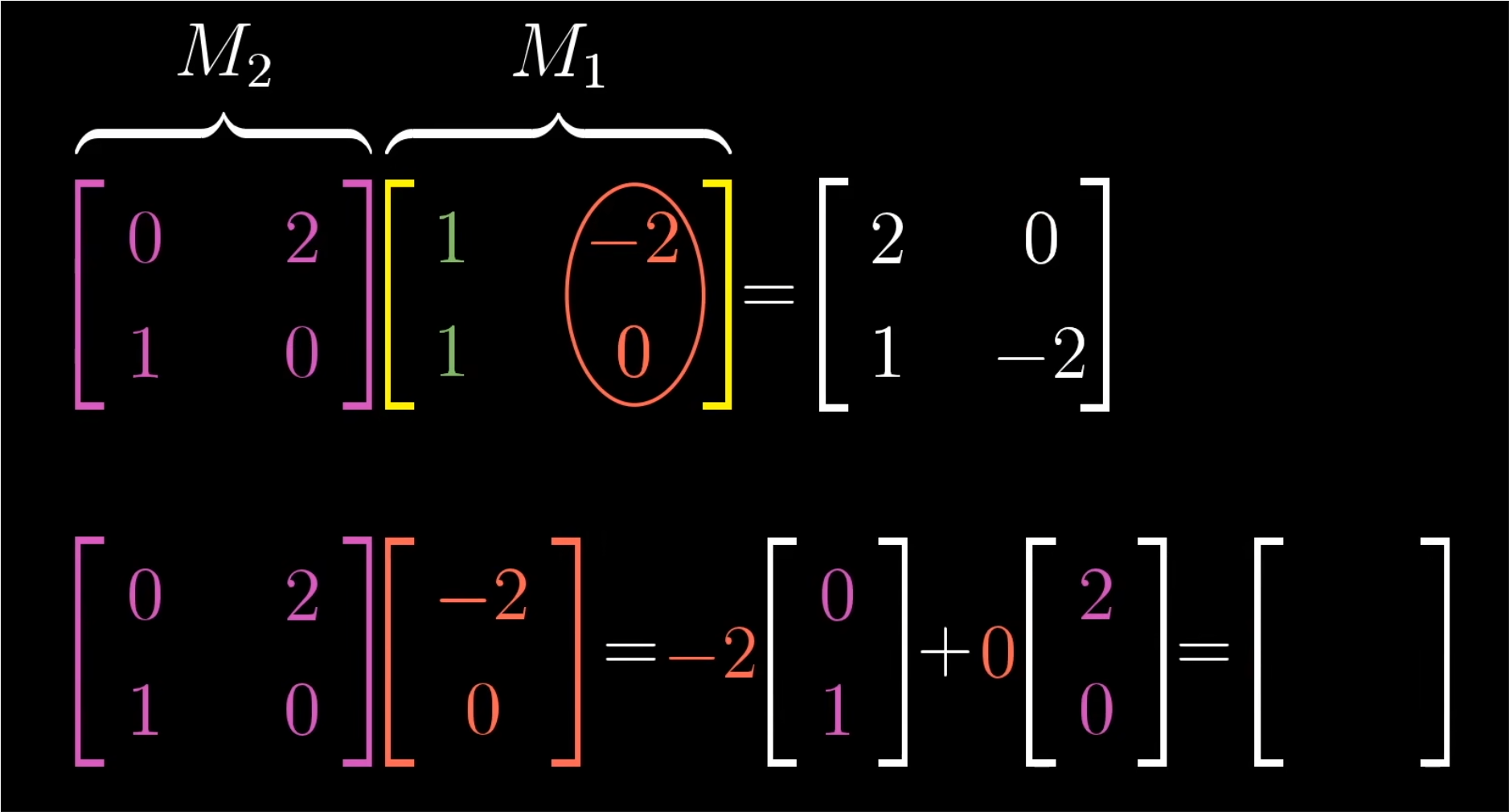
    复合矩阵示例_j帽变换
  • 这一推理具有普适性，对任意矩阵都适用。
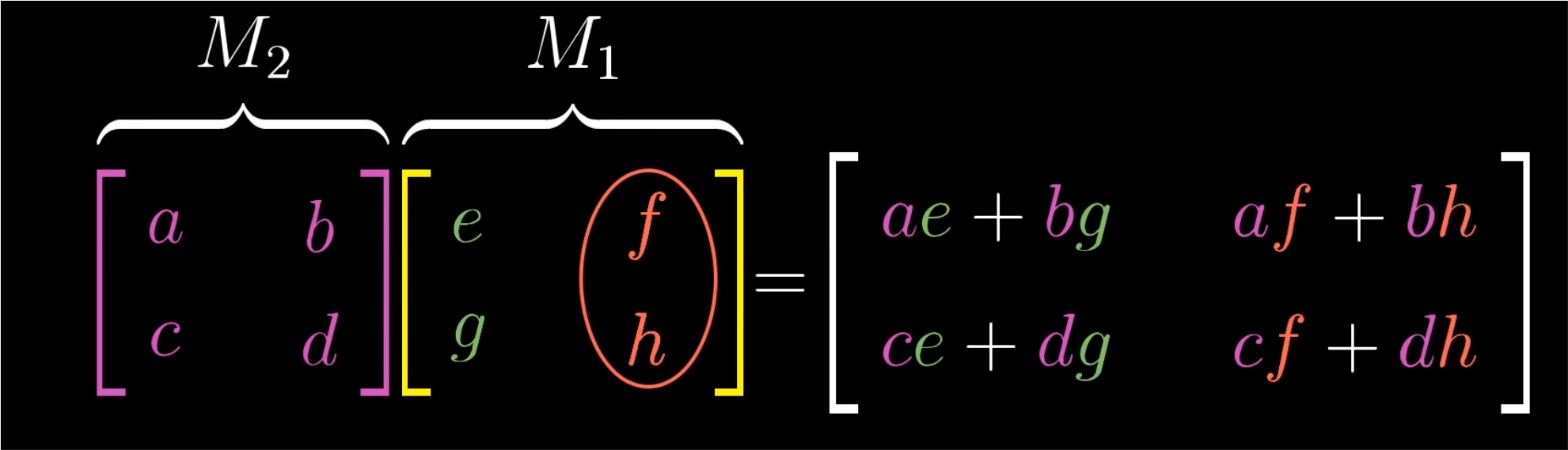
    矩阵乘法公式

✍️注意矩阵计算顺序不可对调：

  • 矩阵乘法不具有交换律。
  • 如之前的推导公式中，M1M2≠M2M1；即在矩阵运算中“先剪切，后旋转”并不等于“先旋转，后剪切”。
  • 乘积顺序影响整体的计算。

✍️结合律（Associativity）：

  • 矩阵乘法满足结合律。
  • A（BC） = （AB）C
  • 空间变换来看，线性变换的作用对象是向量，这个计算是线性变换的复合，而不是指把一个作用于另一个。
  • 以上的等式左边是在说：首先应用C变换和B变换，然后应用A变换；等式右边还是在说：首先应用C变换，其次应用B变换和A变换。
  • 这只是将同样的三个变换用同样的顺序依次总用，换句话说就是：添加括号与结果无关，他们的计算顺序没有变化（记住矩阵变换始终是从右往左读的）。括号的意义在这里表示某两个要一起做，而不是他们做的顺序提前。

✏️三维空间中的线性变换：

  • 考虑这样一个线性变换，他以三维向量为输入，并以三维向量为输出；我们可以想象他在移动三维空间中的所有点，保持网格线平行且等距分布，并保持原点不动。
  • 和二维的情形一样，我们看见三维空间中每一个点实际上只是用来代表以它本身为终点的一个向量；而我们所做的变换只是将输入向量移动至对应向量。
  • 三维线性的变换由基向量的去向完全决定。
  • 此时就有3个基向量，分别是x方向的i帽，y方向的j帽，z方向的k帽。
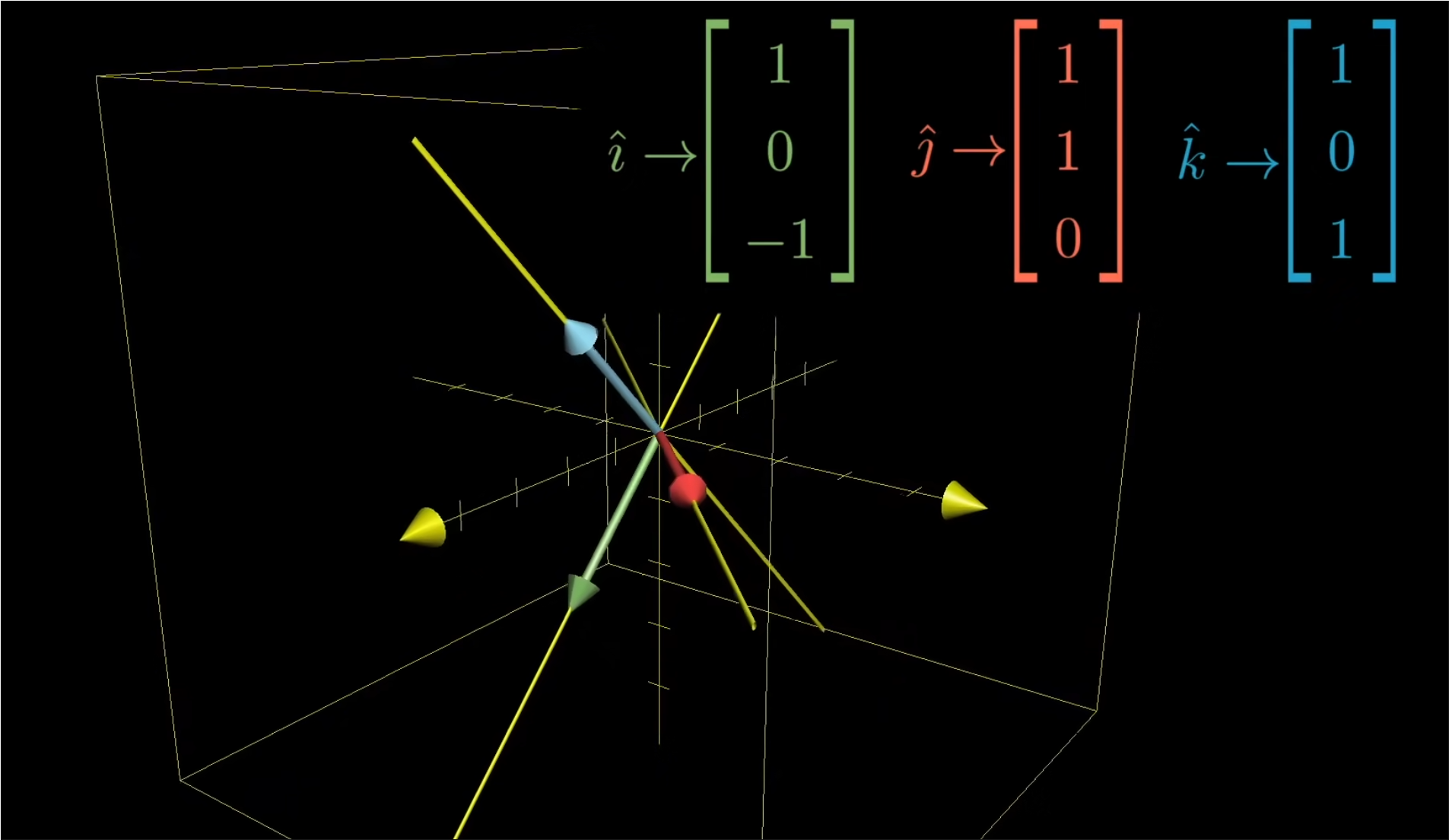
    三维空间的变换
  • 将变换后的三个基向量的坐标记录在一个3x3的矩阵中。这九个数字就完全描述了一个线性变换。
  • 三维空间内向量的变换公式推导与二维空间几乎一致，它每个坐标都可以看作对相应基向量的缩放。
    3x3矩阵变换
  • 3x3矩阵的运用十分广泛,如计算机图形学（Computer Graphics）与机器人学（Robotics）。