3Blue1Brown_线代本质第五章:行列式
3Blue1Brown_线代本质第五章:行列式
- 我开始了3蓝1棕的线性代数本质的学习,我没什么基础所以在此做了笔记,这里是第五章打卡,学习永远不怕晚哈!如有问题请各位大佬及时指正!
- 在b站它的链接在此。
- 官方一共将此系列分为12节,所以我也会分开写。
- 我会把相关的这一系列笔记链接在每一篇的最下面,写完就会更新,有需要的朋友可以自行跳转!
- 这就是普通的记录,比较基础,没什么有新意的地方。厉害的大佬或相关专业的大佬可以自行跳过此笔记!
✏️区域内面积增大减小:
- 想象一些线性空间,有的变换是向外拉伸空间(Generally stretches space),有的则是向内挤压(Generally squashes space);有件事情对理解这些线性变换很有用,那就是测量这些变换究竟对空间有多少拉伸或挤压;也就是:测量一个给定区域面积增大或减小的比例。

- 如上图所示,i帽从(1,0)变换为(3,0),j帽从(0,1)变换为(0,2);则由i帽和j帽决定的单位正方形的面积从原先的1x1变成了现在的3x2;它的面积增大了6倍。所以我们说这个线性变换将它的面积变为6倍。

- 【剪切矩阵】则是i帽不变还是在(1,0),j帽从(0,1)变为(1,1);此时由i帽和j帽决定的单位正方形在变换后倾斜为一个平行四边形,但是它的面积是不变的。所以说即便这个变换空间向右挤压,它并不改变面积。
- 实际上,只要知道单位正方形面积变化的比例,他就能告诉你其他任意区域的面积变化比例(因为“网格线保持平行且等距分布”)。
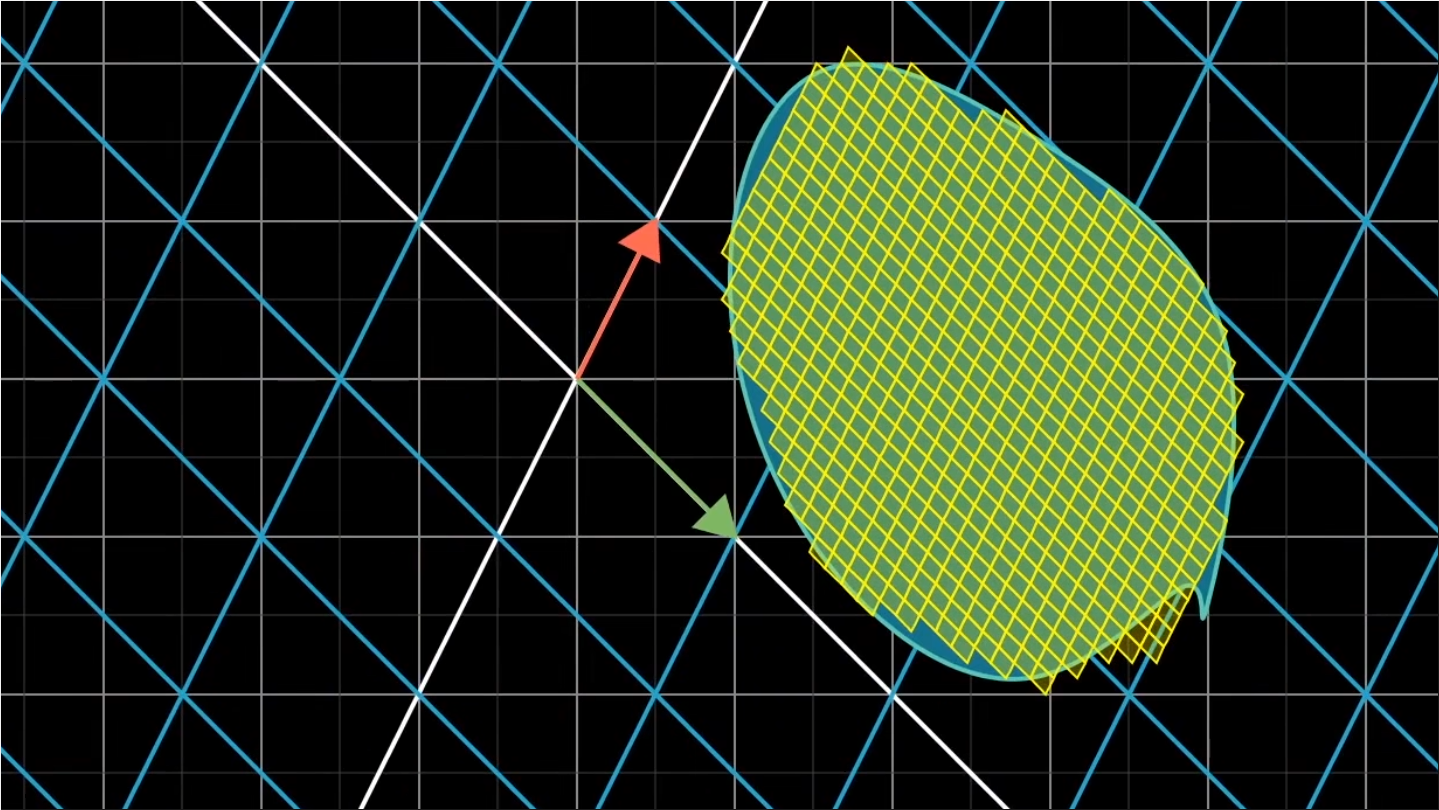
- 对于不是方形网格的形状,我们可以用许多放个良好近似,只要使用的方格足够小,近似就能足够好。由于所有的小方格都是进行等比缩放,所以整个形状也进行了同样比例的缩放。
✏️线性变换的行列式(The “deternminant” of a transformation):

- 比如说,一个线性变换的行列式是3,那么就是说他将一个区域的面积增加为原来的三倍。
- 同理一个线性变换的行列式是1/2,那么就说他将一个区域的面积减少为原来的二分之一。
- 如果一个线性变换的行列式是0,那么说明它将整个平面压缩到一条线,甚至是一个点上。
- 如果变换前j帽在i帽的左侧,变换后j帽变成i帽的右侧,那么此时空间定向就发生了改变(Orientation has been reversed)。
- 当空间定向改变,行列式为负,但是行列式的绝对值依然表示区域面积的缩放比例。
✍️负的面积为什么与定向改变相关?
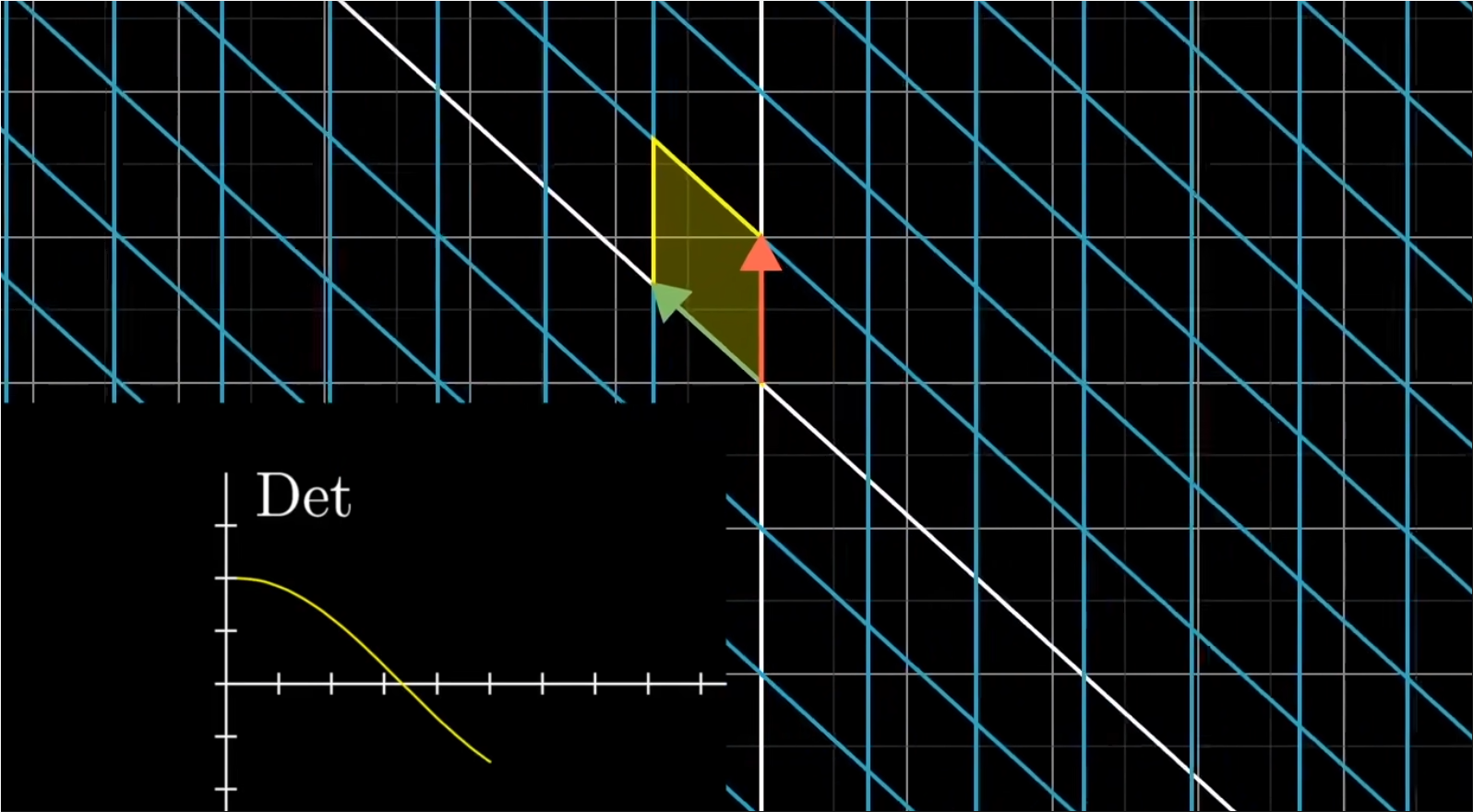
- 考虑i帽靠近j帽时的变换,空间也被更厉害的压缩,意味着行列式趋近于0;当i帽与j帽完全重合时,行列式为0。如果i帽继续沿着这个方向运动,则行列式继续减小为负值。
✏️三维空间中行列式的变换:

- 它告诉你的依然是变换前后的缩放比例,不过三维空间内缩放的是体积。
- 在三维空间中我们可以用1x1x1,即i,j,k这三个基向量,这个特殊的立方体来观察行列式的变换。
- 我们可以把行列式简单的看作这个平行六面体的体积
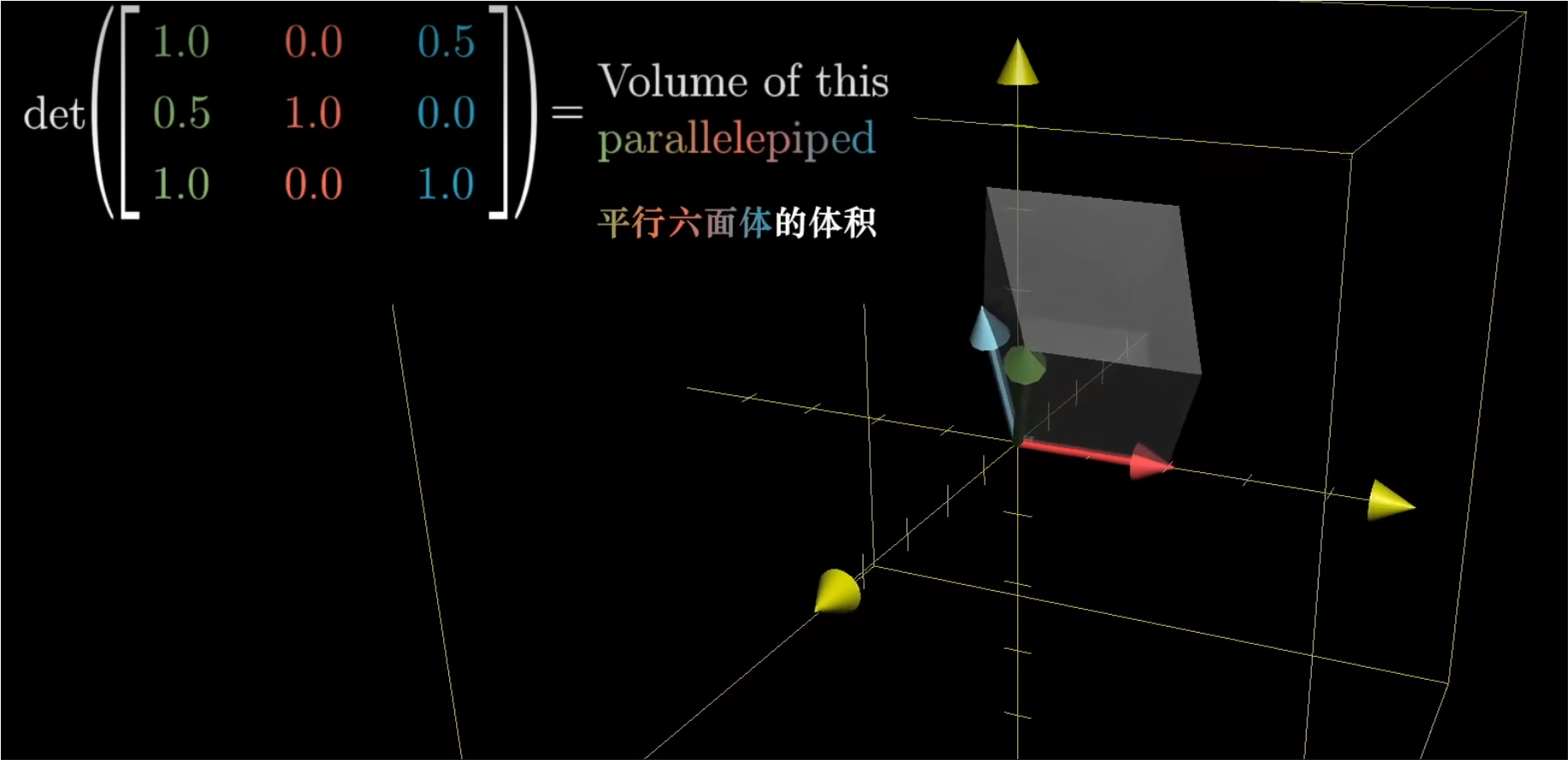
- 行列式为0则意味着整个空间被压缩为零体积的东西。也就是一个平面,一条直线或一个点。
✍️如何计算行列式?:
- 首先它必须得是方形矩阵(行列数相等)。
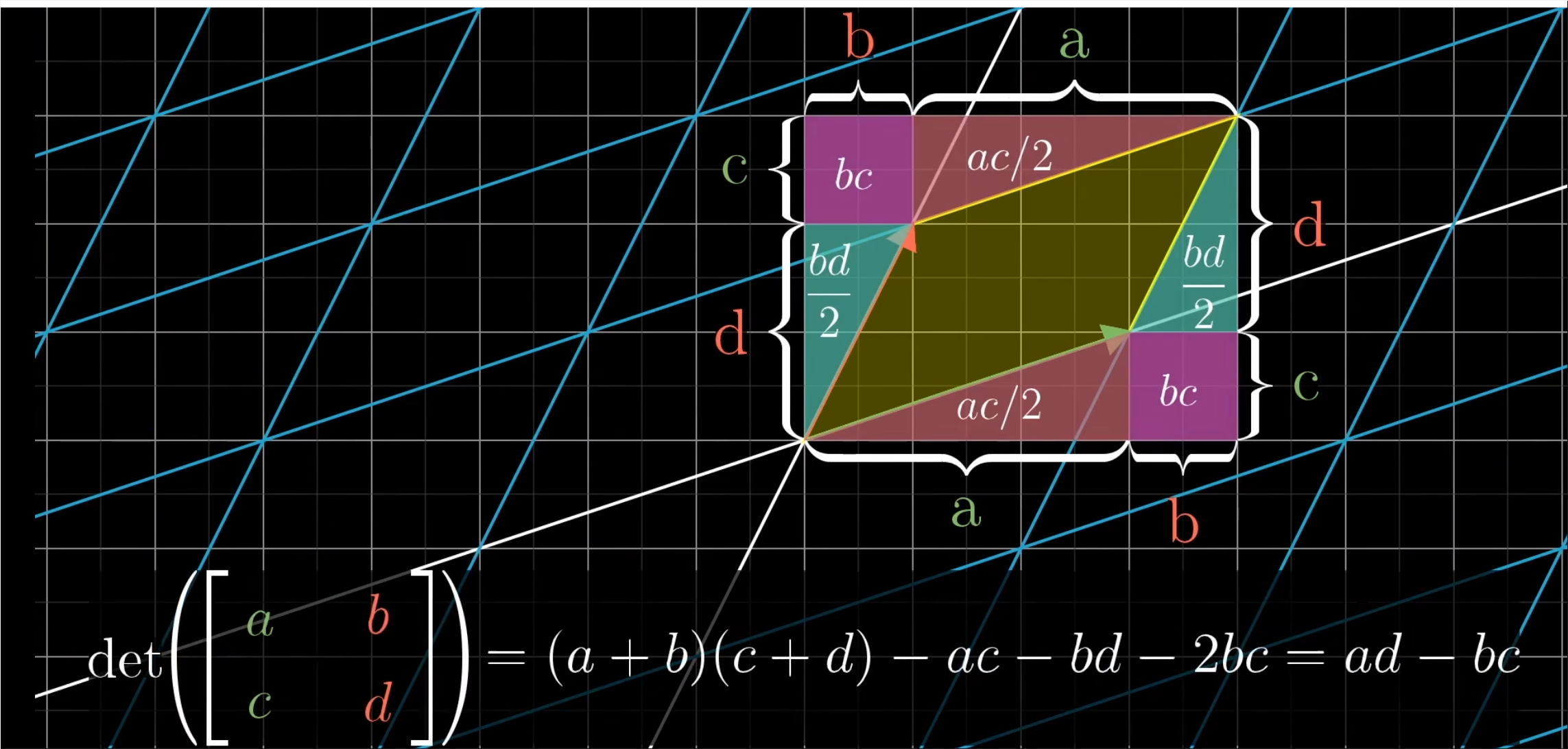
- ad是平行四边形的面积公式底乘以高,如果c不为0的情况下,这个bc项准确的告诉你平行四边形在对角线方向上拉伸或压缩了多少;则这个公式就可以计算出拉伸后的面积。
✍️三阶行列式计算公式:
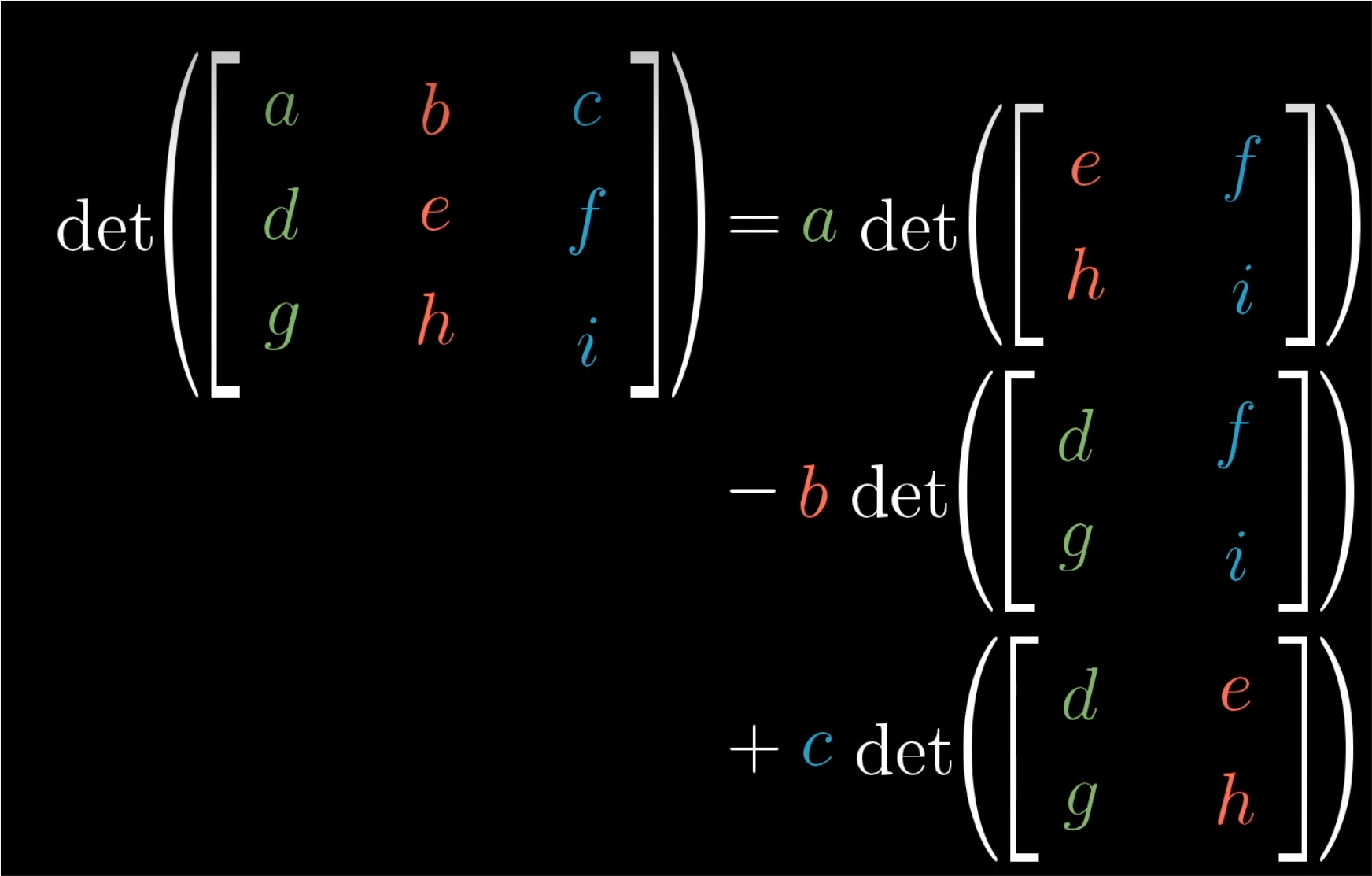
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 ZeTiiCannotStop!
评论






