【注：本章笔记是第六章加附注二的笔记，也就是《逆矩阵，列空间与零空间》加《非方阵》。】

3Blue1Brown_线代本质第六章：逆矩阵，列空间与零空间

  • 我开始了3蓝1棕的线性代数本质的学习，我没什么基础所以在此做了笔记，这里是第六章打卡，学习永远不怕晚哈！如有问题请各位大佬及时指正！
  • 在b站它的链接在此。
  • 官方一共将此系列分为12节，所以我也会分开写。
  • 我会把相关的这一系列笔记链接在每一篇的最下面，写完就会更新，有需要的朋友可以自行跳转！
  • 这就是普通的记录，比较基础，没什么有新意的地方。厉害的大佬或相关专业的大佬可以自行跳过此笔记！

✏️逆矩阵（Inverse Matrices）：

✍️矩阵的用途：

  • 操纵空间，并且线性代数几乎在所有技术领域都有体现。
  • 它能帮助我们求解特定的方程组。
  • 如果一个特定的方程里面它只存在常数和未知变量（没有幂，没有奇怪的函数，没有未知量间的乘积等等），我们整理这个方程组，将未知量放在左边，常数项放在右边；如果能对其未知变量就更好（必要情况下添加系数0）；此时，就被称为“线性方程组”（Linear system of equations）
  • 此时我们可以将此整合成一个含有常数系数和未知变量的矩阵，以及他们乘积所得到的一个常数向量。
  • （注意：此时先将范围限制在方程数目与未知量数目相等的情况内）
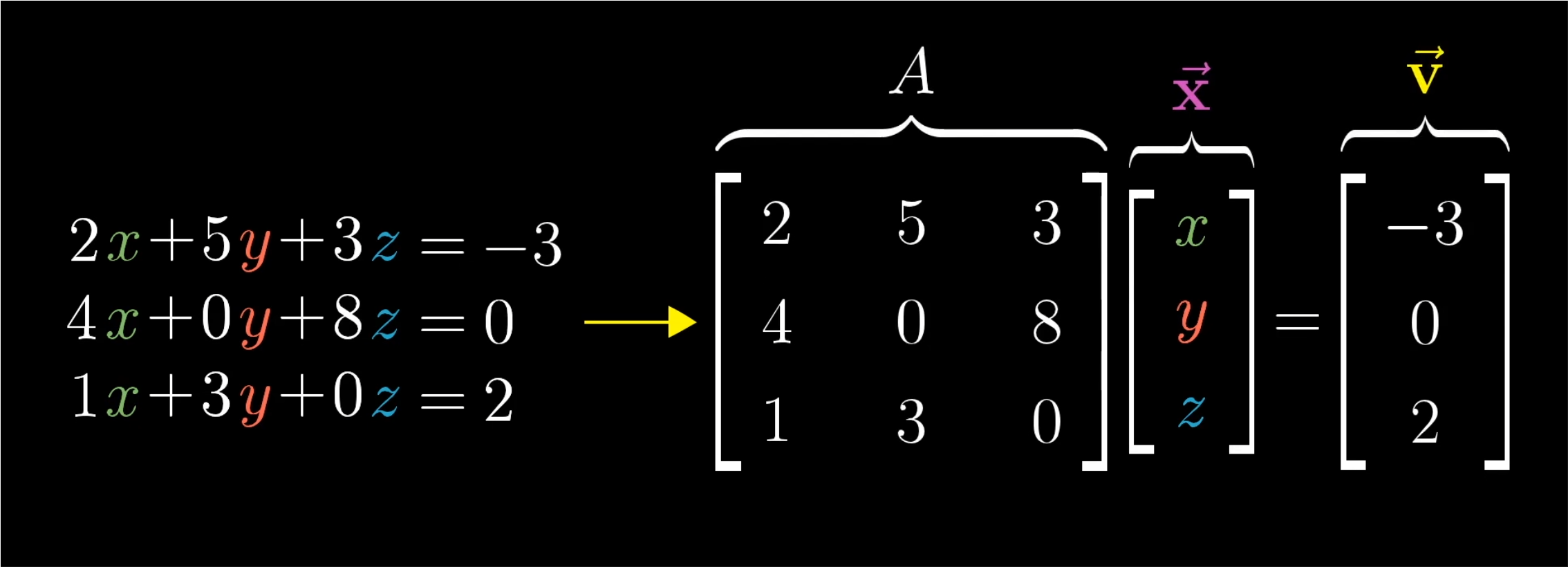
    方程组和矩阵
  • 如上图，我们称系数矩阵为A，包含未知数的向量为粗体x，右侧的常数向量为v。这不仅仅是将方程组写进一行的书写技巧，它还阐明了这个问题中优美的几何直观部分。
  • 矩阵A代表一种线性变换，所以求解Ax=v意味着我们去寻找一个向量x，使得它在变换后与v重合。
  • 所以求解此方程组，我们完全可以只考虑对空间的变换，以及变换后向量的重叠。

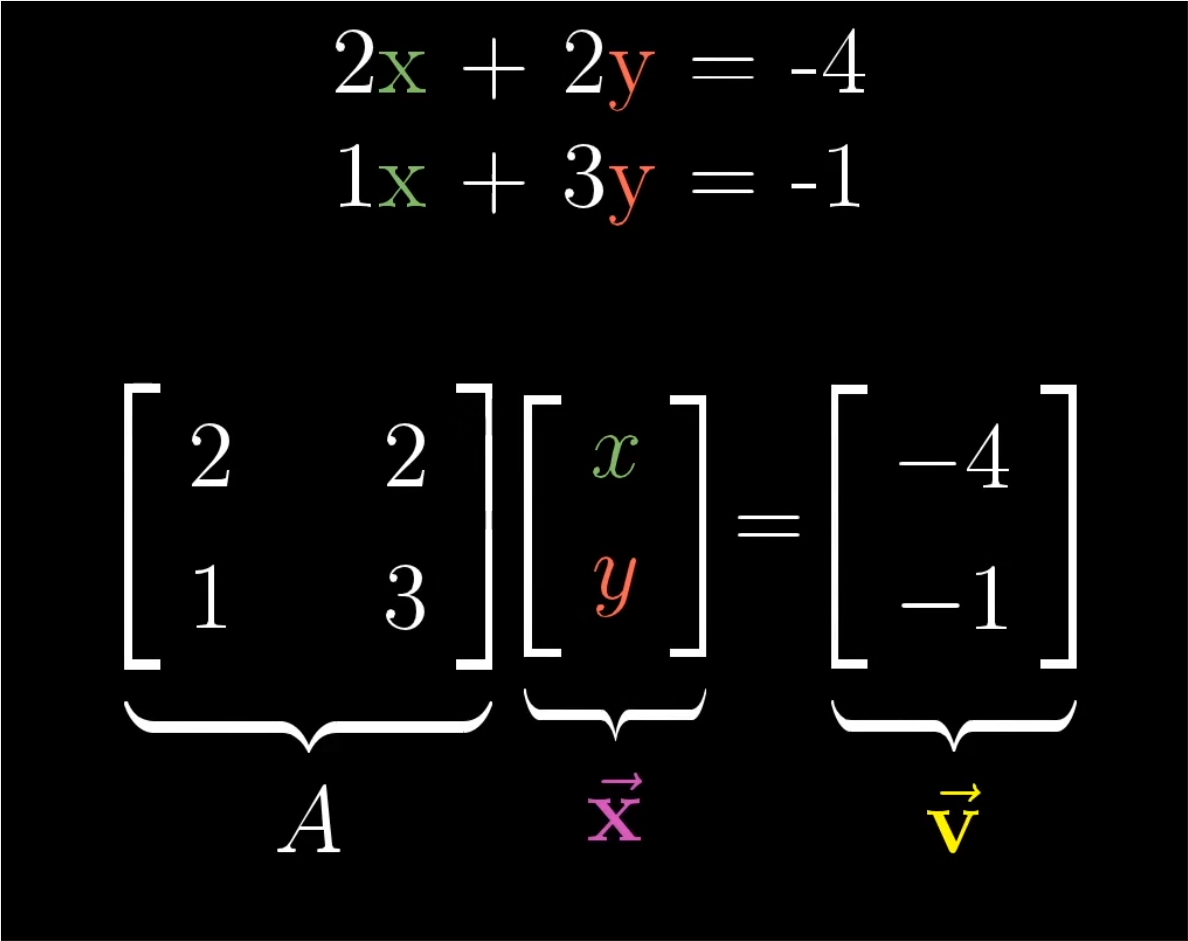
两个未知量构成的方程组

  • 现在上图这个含有两个未知量构成的方程组，它的解依赖于矩阵A所代表的变换。
  • 将空间挤压到一条线或一个点等低维空间，A保持空间为2维。
  • 我们将它们分为两种情况：
    1. A的行列式为0。
    2. A的行列式不为0。

A的行列式不为0的情况：

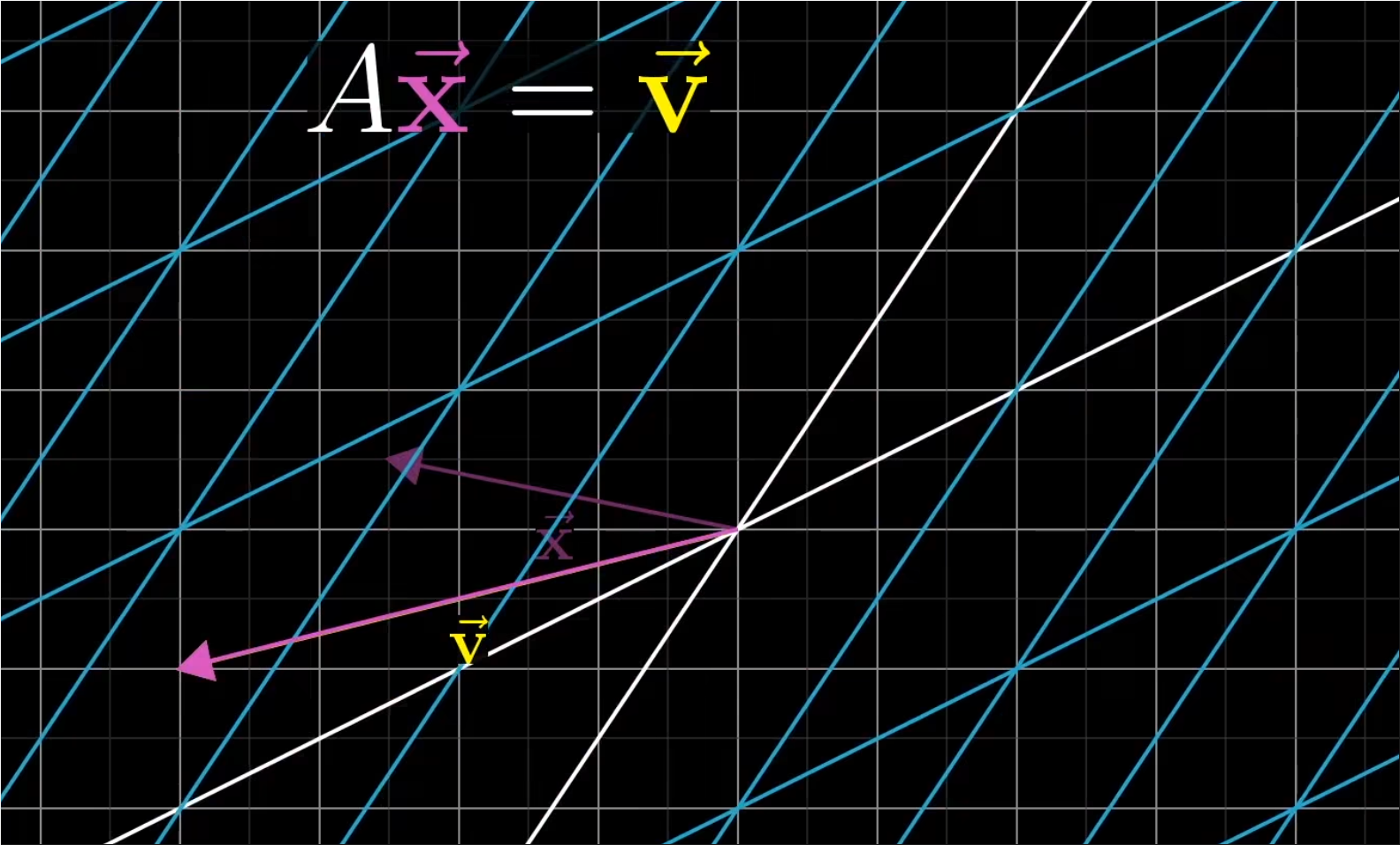
A的行列式不为0

  • 这种情况下，有且只有一个向量在变换后与v重合，并且可以通过逆向进行变换来找到这个向量。如同倒带一样，通过跟踪v的动向，就能找到满足Ax=v的向量x。
  • 当你逆向进行变换时，它实际上对应了另一个线性变换，通常被称为“A的逆”，记为A^(-1)。
  • 这个过程在几何上就对应与逆向进行变换并跟踪v的动向。
    A的逆
  • 随机选一个矩阵，有很大的可能会遇到这一非零行列式的情况。也就是说，对于两个未知量和两个方程所构成的方程组存在它唯一的解。
  • 当方程树木与未知量数目相同时，这一思想在高维情况下也有意义。同样也可以给方程组赋予几何意义。
  • 只要保证A不将空间挤压到一个更低的维度，那么就是A的行列式不为零的情况，那他就存在逆变换（A逆）。这使得应用A变换在应用A逆变换之后，结果恒等。

A的行列式为0的情况：

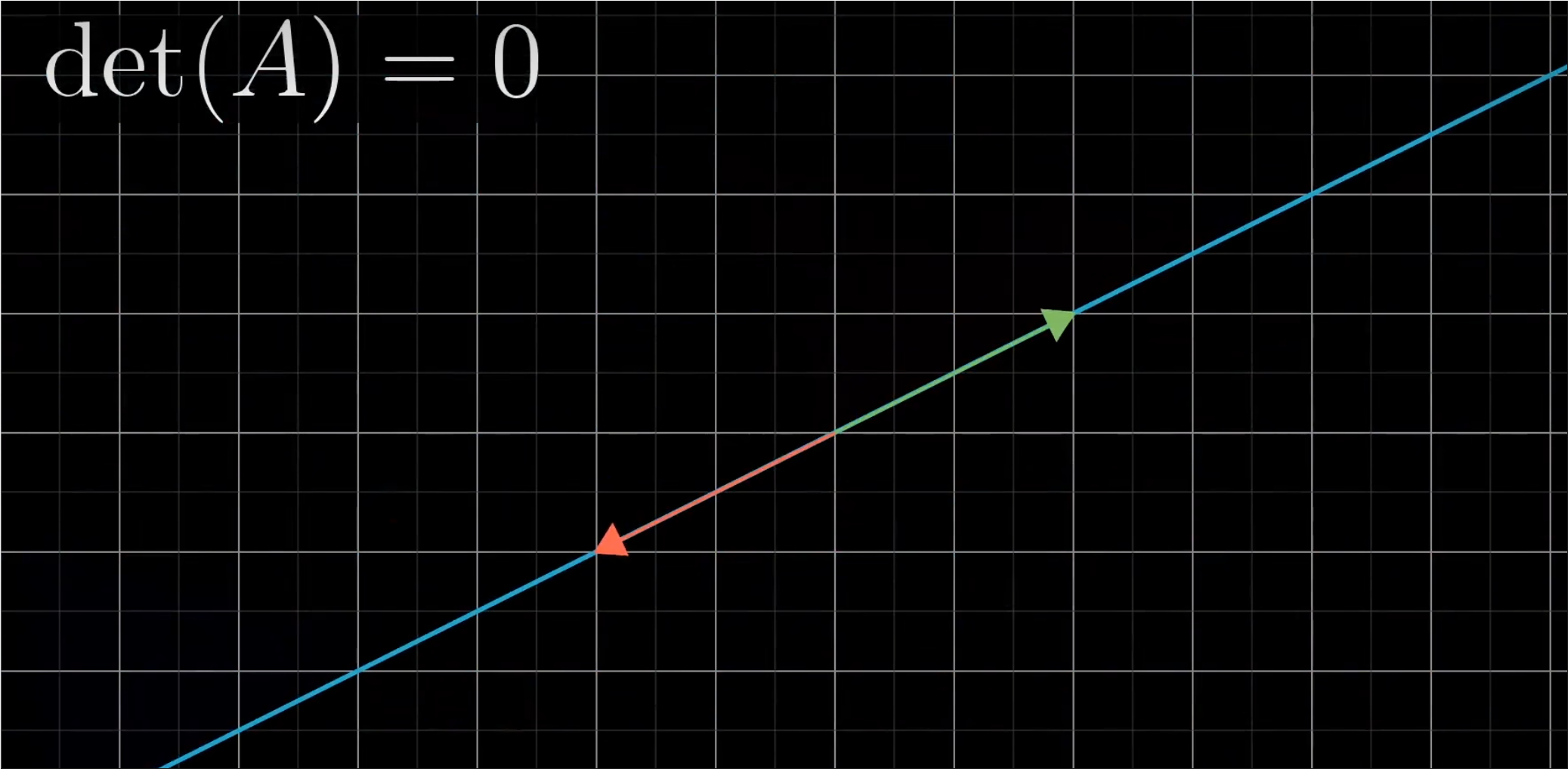
A的行列式为0

  • 这个方程组相关的变换会压缩到更低的维度。
  • 此时不存在逆变换，函数无法将一条线变换回一个平面。
  • 此时的解依旧存在，向量v很可能恰好处于这条线上。三维空间时，解的存在难度就会更高。

✏️秩（rank）：

  • 当变换结果为一条直线时，也就是说结果是一维的，我们称这个变换的秩为1（Rank1）。
  • 如果变换后的向量落在某个二维平面上，我们称这个变换的秩为2（Rank2）。
  • 所以说“秩”代表着变换后空间的维数。
  • 所以说对于2x2的矩阵，它的秩最大为2，意味着基向量仍旧能张成整个二维空间，并且矩阵的行列式不为0。
  • 如果对于3x3矩阵来说，秩为2的时候意味着空间被压缩了，和秩为1的情况下相比较，压缩的并不是那么严重。
  • 如果一个三维变换的行列式不为0，变换结果仍旧充满整个三维空间，那么它的秩为3。

✏️列空间（Column Space）：

矩阵的列空间

  • 无论是一条直线，一个平面还是三维空间，所有可能变换结果的集合被称为矩阵的“列空间”（Column Space）。
  • 这个来源很简单，矩阵的列告诉你基向量变换后的位置。这些变换后的基向量张成的空间就是所有可能的变换结果。换句话说，列空间就是矩阵的列所张成的空间。
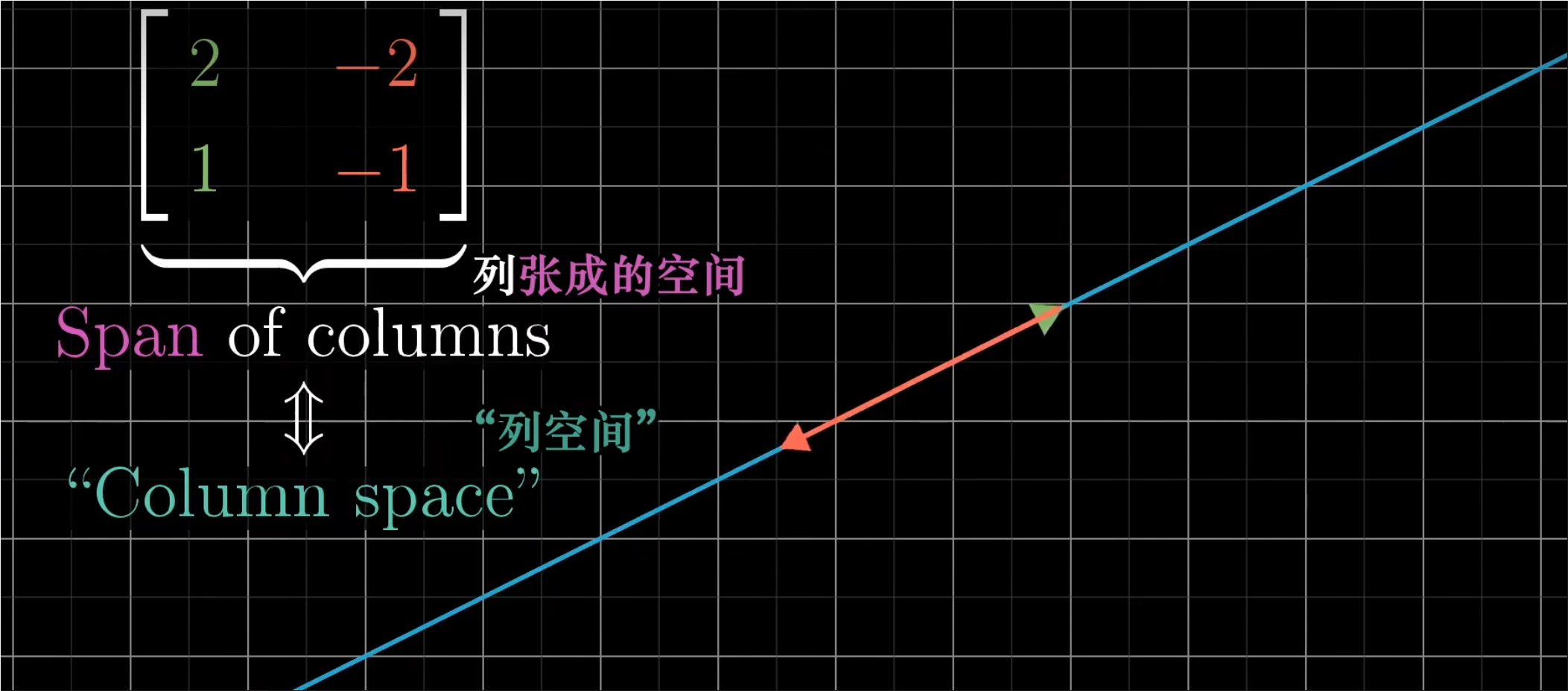
    列张成的空间
  • 所以更精确的说，秩的定义是列空间的维数。
  • 当秩达到最大值时，意味着秩与列数相等，我们称之为“满秩”（Full Rank）

✍️零空间（Null space）：

  • 需要注意的是，零向量一定会被包含在列空间中，因为线性变换必须保证原点位置不变。
  • 对于一个满秩变换来说，唯一能在变换后落在原点的就是零向量（0，0）自身。
  • 但是对于一个非满秩的矩阵来说，他将空间压缩到一个更低的维度上，也就是说会有一系列向量在变换后成为零向量（被压缩的空间的有一部分会部分归到0向量）。
  • 这被称为矩阵的“零空间”（Null Space）或“核”（Kernel）。
  • 变换后的一些向量落在零向量上，而“零空间”正式这些向量所构成的空间。
  • 对线性方程组来说，当向量v恰好为零向量时，零空间给出的就是这个向量方程所有可能的解。

✏️总结：

每个方程组都有一个线性变换与之联系。
当逆变换存在时，你就能用这个逆变换求解方程组。
列空间的概念让我们清楚什么时候存在解什么时候不存在。
零空间的概念有助于我们理解所有可能的解的集合。

✏️附注二：

✍️非方阵（Nonsquare Matrices）：

  • 在之前的学习中，使用的几乎都是2x2或者3x3这样的方形矩阵来举例子，但现在需要讨论一下非方阵。
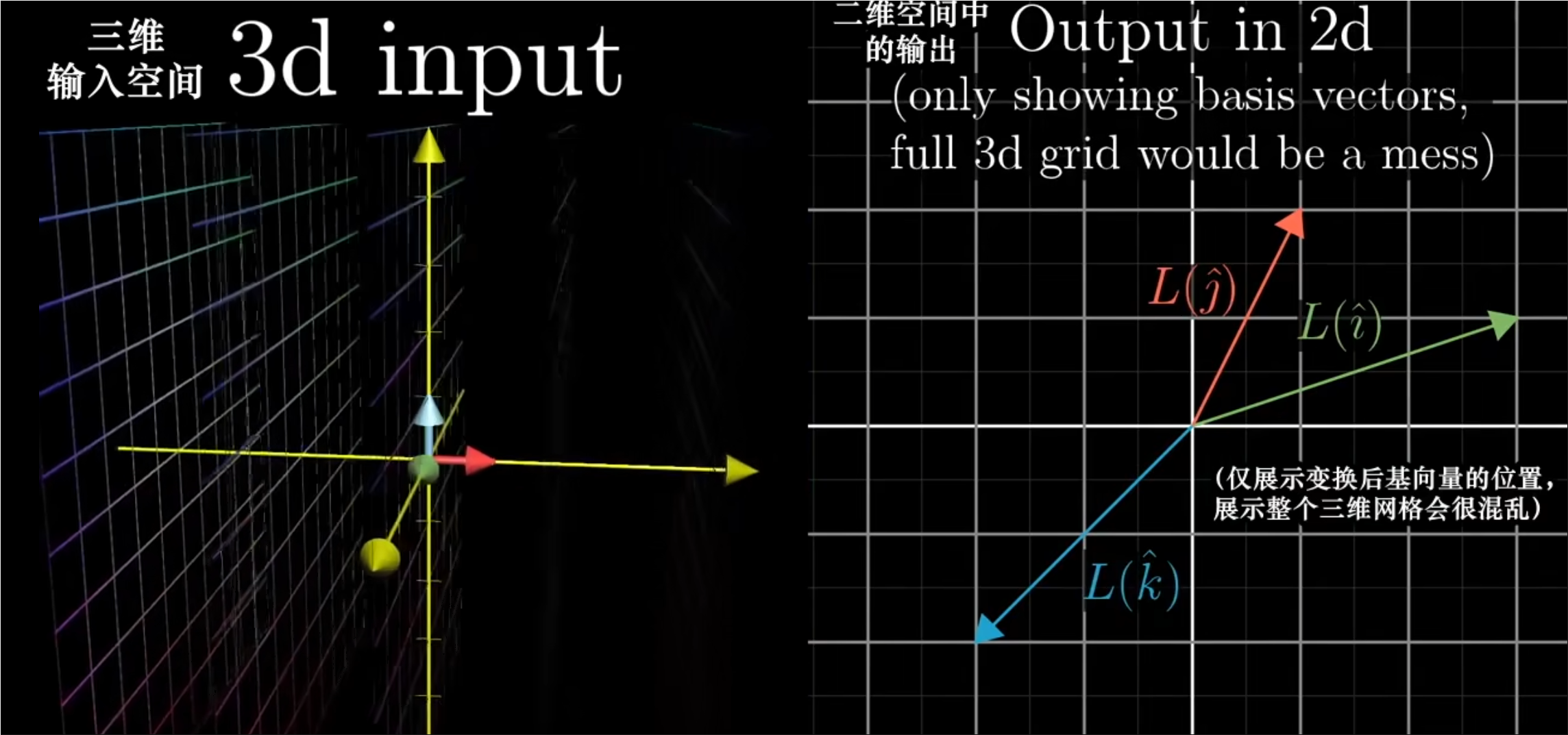
  • 讨论不同维数之间的变换是完全合理的，比如一个二维向量到三位向量的变换。
  • 同之前一样，如果网格线保持平行且等距分布，并且原点映射为自身，就称它为线性的。
    二维向量到三维向量
  • 此时要注意的是，由上图所示，输入的二维向量与输出的三维向量是完全不同的物种，他们生活在没有任何关联的空间当中。

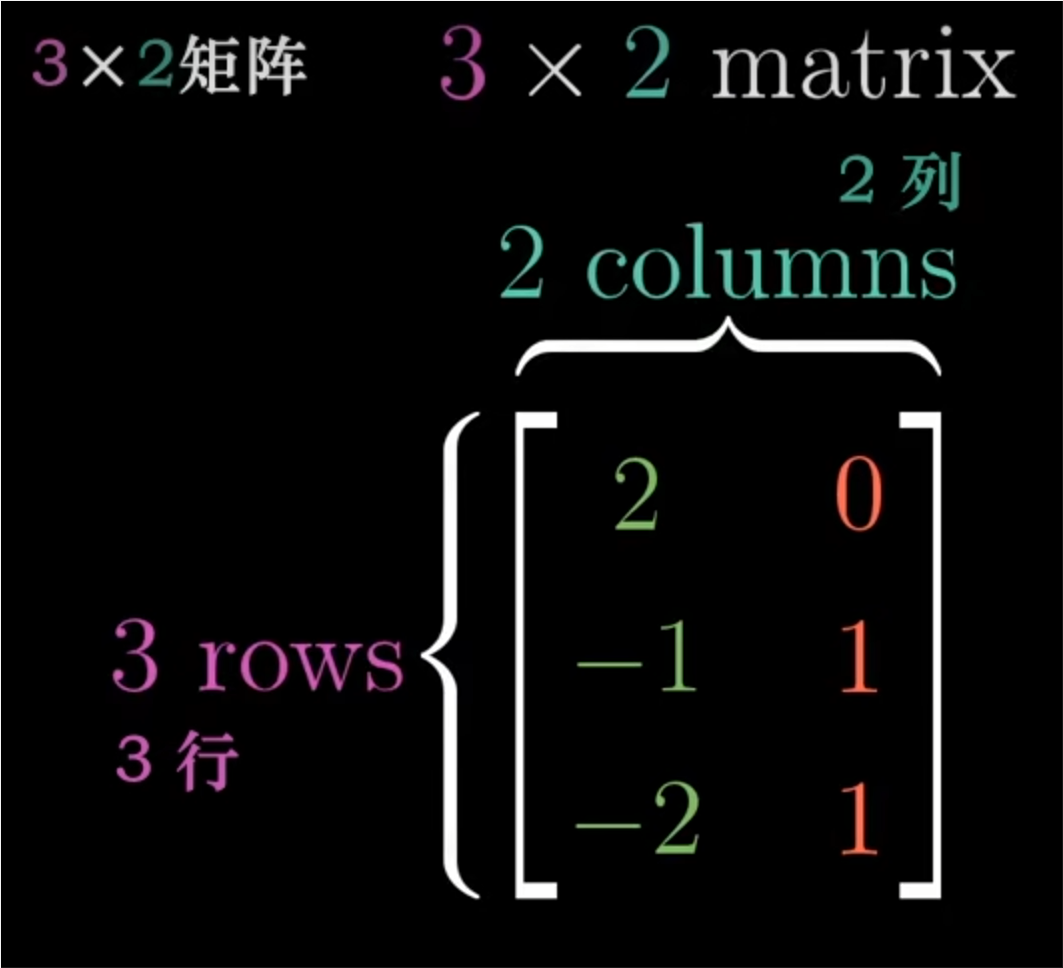
3x2矩阵：

  • 用矩阵代表这样一个变换则和之前相同；找到每一个基向量变换后的位置，然后把基向量的坐标作为矩阵的列。如下图所示。
    变换示例
  • 注意一点，这意味着代表这个变换的矩阵是三行两列，也就是3x2矩阵。这个矩阵的列空间是三维空间中一个过原点的二维平面，但是这个矩阵任然是满秩的。因为列空间的维数与输入空间的维数相等。
  • 它的几何意义是将二维空间映射到三维空间上，因为矩阵有两列表面输入空间有两个基向量，有三行表明每个基向量在变换后都用三个独立的坐标来表示。
    3x2矩阵

2x3矩阵：

  • 类似的，当我们看见一个两行三列也就是2x3矩阵时，表面矩阵有三个基向量，也就是说原始空间是三维的；每个变换后的基向量用两个坐标来表示，所以他们一定落在二维空间。因此这是一个从三维空间到二维空间的变换。如下图所示例。
    2x3矩阵示例

1x2矩阵：

  • 除此以外，当然还可以由二维空间到一维空间的转换，一维空间实际上就是数轴。
  • 这里可以理解为如果一条直线上有一系列等距分布的点，在映射到数轴之后，他们将保持等距分布，这样的变换也可以用一个1x2矩阵表示，而这个矩阵的两列都只有一个数，这两列分别代表了变换后的基向量。
  • 实际上这是一类非常有意义的变换，它与点积紧密相关。
    1x2矩阵