3Blue1Brown_线代本质第九章：基变换

我开始了3蓝1棕的线性代数本质的学习，我没什么基础所以在此做了笔记，这里是第九章打卡，学习永远不怕晚哈！如有问题请各位大佬及时指正！
在b站它的链接在此。
官方一共将此系列分为12节，所以我也会分开写。
我会把相关的这一系列笔记链接在每一篇的最下面，写完就会更新，有需要的朋友可以自行跳转！
这就是普通的记录，比较基础，没什么有新意的地方。厉害的大佬或相关专业的大佬可以自行跳过此笔记！

✏️基变换：

✍️基的选择：

发生在向量与一组数之间的任意一种转化，都被称为一个坐标系（coordinate system），而其中两个特殊的向量i帽和j帽，被我们称为这个标准坐标的基向量。
如上图所示，如果使用另一组不同的基向量，分别称之为b1和b2，它的第一个基向量b1指向右上方，第二个基向量b2指向左上方。如果在这个变换中，用坐标（5/3.1/3）来描述它，这意味着，根据他的两个基向量，获得那个向量的方法是b1乘以5/3,b2乘以1/3,再将两个结果相加。
总之，无论何时，我们用坐标来描述一个向量，将第一个坐标乘以b1，第二个坐标乘以b2，然后将两者相加，他最终得到的向量，会和我们认为的相同坐标的向量完全不同。
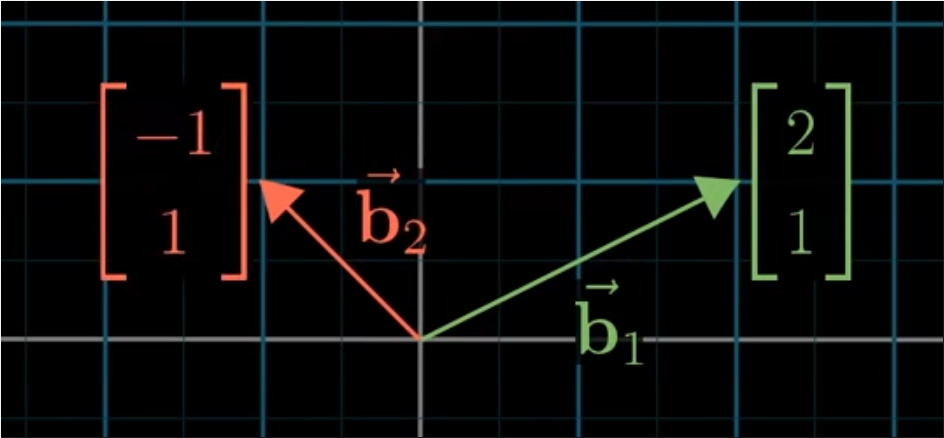
如上图两个向量的表示方法看出，虽然我们都在关注空间中同一个向量，但可以用不同的语言（空间）和数字来描述它，使得结果大不相同。
如果我们使用普通的坐标系，并用方形网格表示单位，那么这些网格只是提供了一个可视化坐标系的途径，因此，它依赖我们对基的选择。因为在空间中，本身是没有网格的。
如果用不同的方式绘制这个网格，它同样是一个框架，也只不过是有助于用另一种方式理解坐标含义的可视化工具。
但是无论如何绘制这个网格，大家的原点总会是在（0，0），因此大家的原点是重合的。 它就是任何向量乘以0时你所得到的坐标。
但是，其他方式绘制的坐标轴的方向与网格间距有所不同，这依赖于它对基的选择。

✍️如何在不同的坐标系之间进行转化？：

一旦你将矩阵向量乘法理解为应用一个特定的线性变换，就会有一种非常直观的方法来考虑这里发生的事。
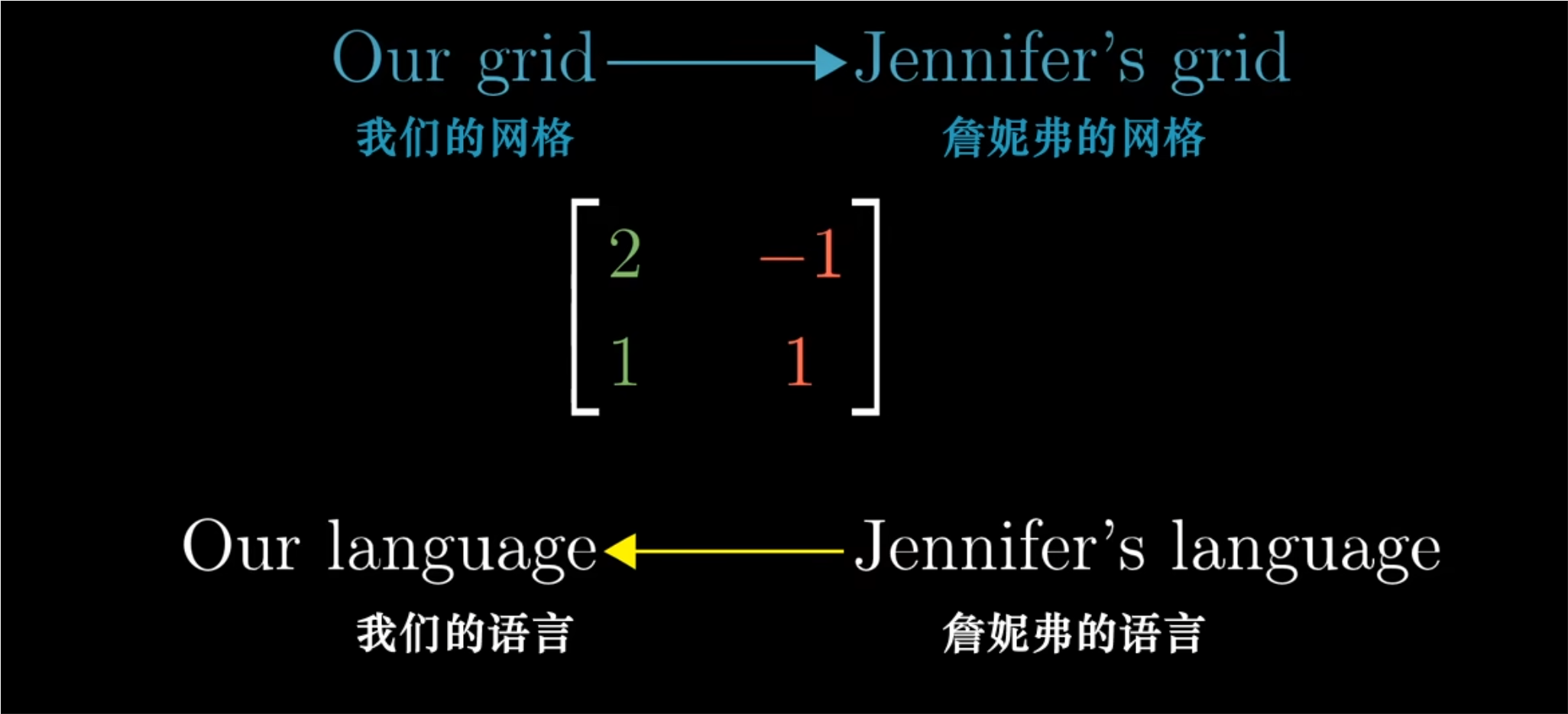
一个矩阵列为某个特殊的基向量时，这个矩阵可以看作一个线性变换，它将我们的基向量i帽和j帽，也就是我们眼中的（1，0）和（0，1），变换为那个特殊的基向量，也就是特殊被重新定义的（1，0）和（0，1）.
变换后的向量仍旧时相同的线性组合，不过使用的时新的基向量。

✍️逆（Inverse）：

一个变换的逆是一个新的变换，它将所选的变换逆向进行。实践当中，尤其是在超过二维空间中研究时，你可以用计算机来计算矩阵的逆。
如果想知道一个矩阵变换的逆，那我们用这个基变换矩阵的逆乘以我们所使用的向量。
以上就是如何在坐标系之间对单个向量的描述进行相互转化。
一个矩阵代表的是一个特殊的基向量，却用我们的坐标来描述；对于一个向量，这个矩阵将它的语言描述转化为我们的语言描述。
逆矩阵则与之相反。
向量并不是唯一用坐标表示的东西

考虑某个线性变换，譬如逆时针旋转90度；用矩阵代表它的时候，我们是在跟踪i帽和j帽的去向；i帽变换后坐标是（0，1），j帽变换后坐标是（-1，0）；这些坐标也就成为了矩阵的列。
但是这种表示与我们对基向量的选择密切相关，因为我们跟踪的是i帽和j帽，并且是在我们自己的坐标系中记录着他们的去向。

✍️如何转化一个矩阵？：

注：以下描述的我们的语言是我们使用的语言，代表我们使用的基向量和坐标系；另一种语言表述的变换暂用詹妮弗的语言代替，詹妮弗跟我们使用不同的坐标系和基向量。

我们从詹妮弗的语言描述的任意向量出发。
首先，我们不用它的语言描述这一过程，而是用基变换矩阵，转化为用我们的语言描述。这个矩阵的列代表是用我们的语言描述她的基向量。此时给出的是同一个向量，只不过是用我们的语言描述的。如下图所示。
然后，将所得结果左乘线性变换矩阵；此时给出的是变换后的向量，但仍然是我们的语言来描述的。如下图所示。
最后一步，像之前一样将所的结果左乘基变换矩阵的逆，从而得到变换后的向量，然而使用詹妮弗的语言来描述的。如下图所示。

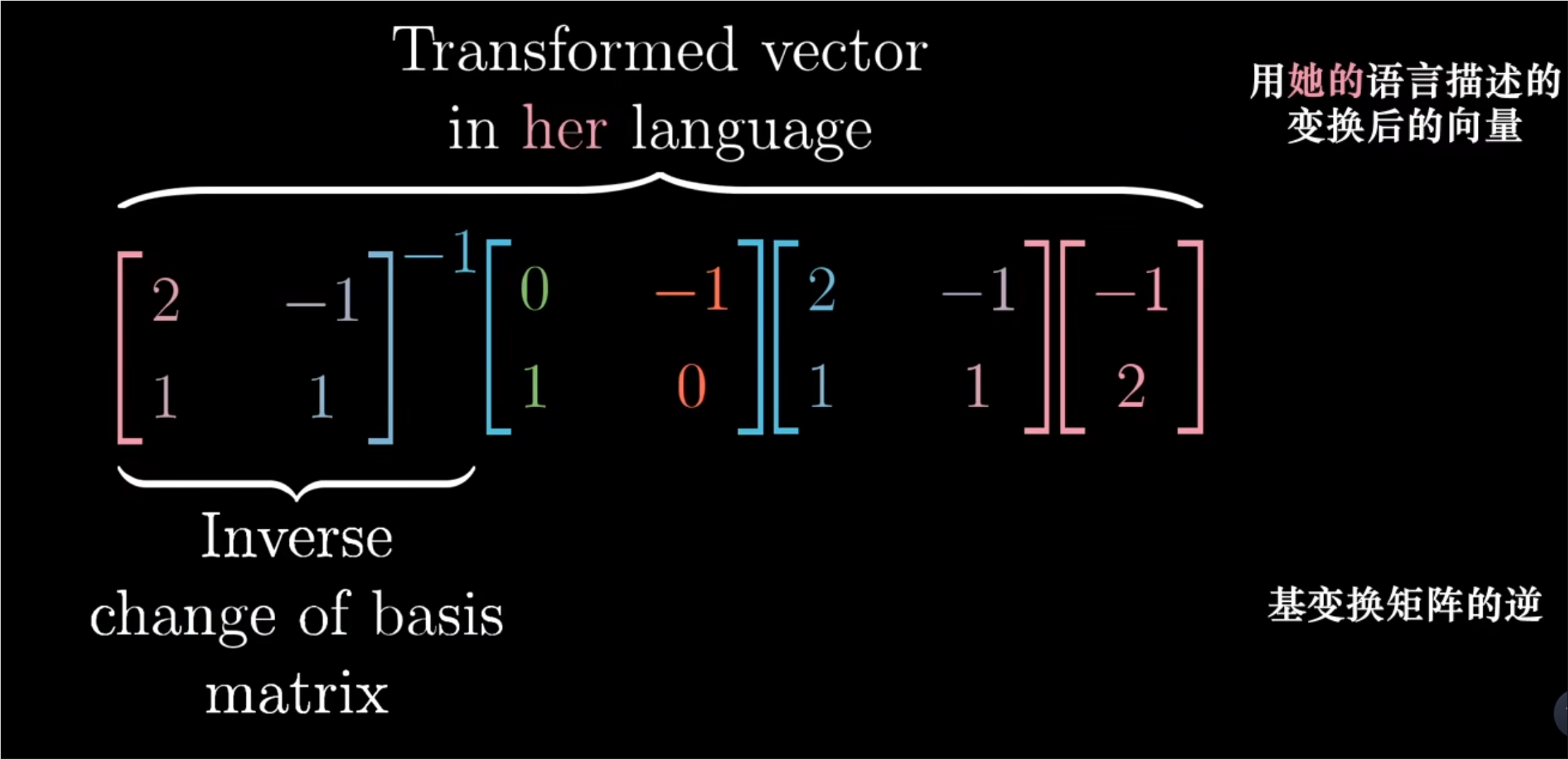
因为我们能够对詹妮弗语言描述的任一向量做同样的事情，首先应用基变换，然后应用线性变换，最后应用基变换的逆。这三个矩阵的复合给出的就是用詹妮弗语言买哦书店线性变换矩阵。它接收由詹妮弗语言描述的向量。，并输出用詹妮弗语言描述的变换后的向量。
所以如果詹妮弗用这个计算结果的矩阵与她坐标系中的一个向量相乘，结果就是在她坐标系中描述该向量旋转90度的结果。