3Blue1Brown_线代本质第十一章:抽象向量空间
3Blue1Brown_线代本质第十一章:抽象向量空间
- 我开始了3蓝1棕的线性代数本质的学习,我没什么基础所以在此做了笔记,这里是第十一章打卡,学习永远不怕晚哈!如有问题请各位大佬及时指正!
- 《线代本质》的内容这一章其实就是完结啦!!!下一章是《克莱姆法则,几何解释》,由于官方账号发在一起了,所以我会把下一章一起当作这个系列的笔记写在一起,所以下一章是第十二章!
- 在b站它的链接在此。
- 官方一共将此系列分为12节,所以我也会分开写。
- 我会把相关的这一系列笔记链接在每一篇的最下面,写完就会更新,有需要的朋友可以自行跳转!
- 这就是普通的记录,比较基础,没什么有新意的地方。厉害的大佬或相关专业的大佬可以自行跳过此笔记!
✏️抽象向量空间:
✍️再来想想什么是向量:
- 坐标的描述是相对随意的,因为这完全依赖于我们所选定的坐标系。
- 行列式告诉你的是一个变换对面积的缩放比例;特征向量则是在变换中留在它所张成的空间中的向量。这二者都是暗含于空间中的性质,可以自由选取坐标系,这并不会改变它们最根本的值。所以:行列式和特征向量与所选坐标系无关。
- 但是,如果向量根本并不是由一组实数构成,它们的本质更具空间性;那么此时,数学中所说的“空间”(space)或“空间性”(spatial)究竟表示什么?
- 所以,我们应当考虑一种:
- 既不是一个箭头,也不是一组数字,但是同样具有向量特征的东西。
✏️函数(function):
✍️函数与向量
- 从某种意义上说,函数实际上只是另一种向量;
- 类比两个向量相加的方法,我们也可以将两个函数f和g相加,从而获得一个新的函数(f+g),这种方式是合理的。如下图所示。
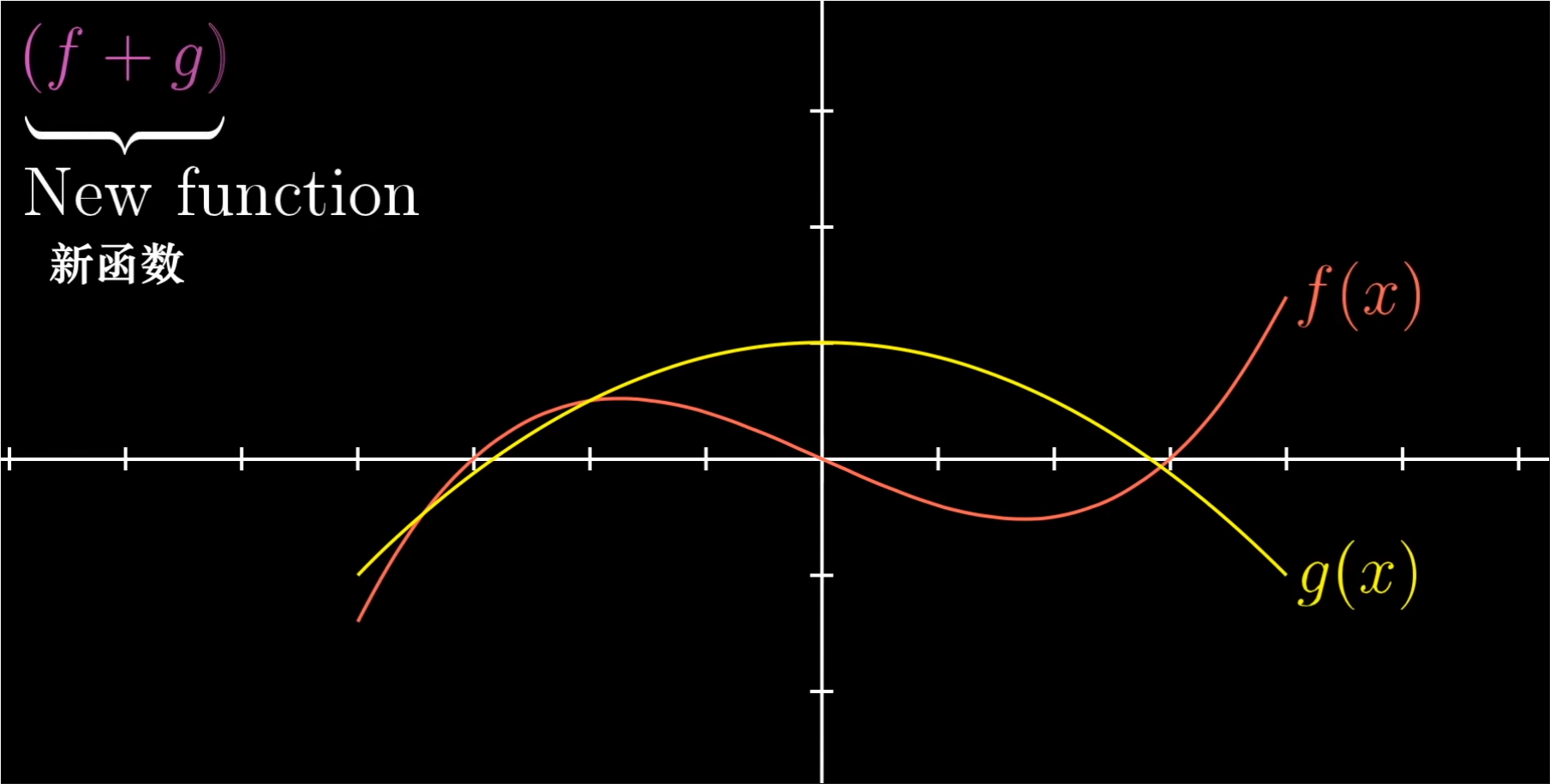
- 这个新函数在任意一点处的值,比如在-4的值,就是f和g在这一点处的值的和。
- 具体一点说,这个和函数在任意一点x处的值(f+g)(x)等于f(x)加上g(x)。
- 这和向量对应坐标相加十分相似;只不过某种程度上来说,它有无穷多个坐标要相加。如下图所示。
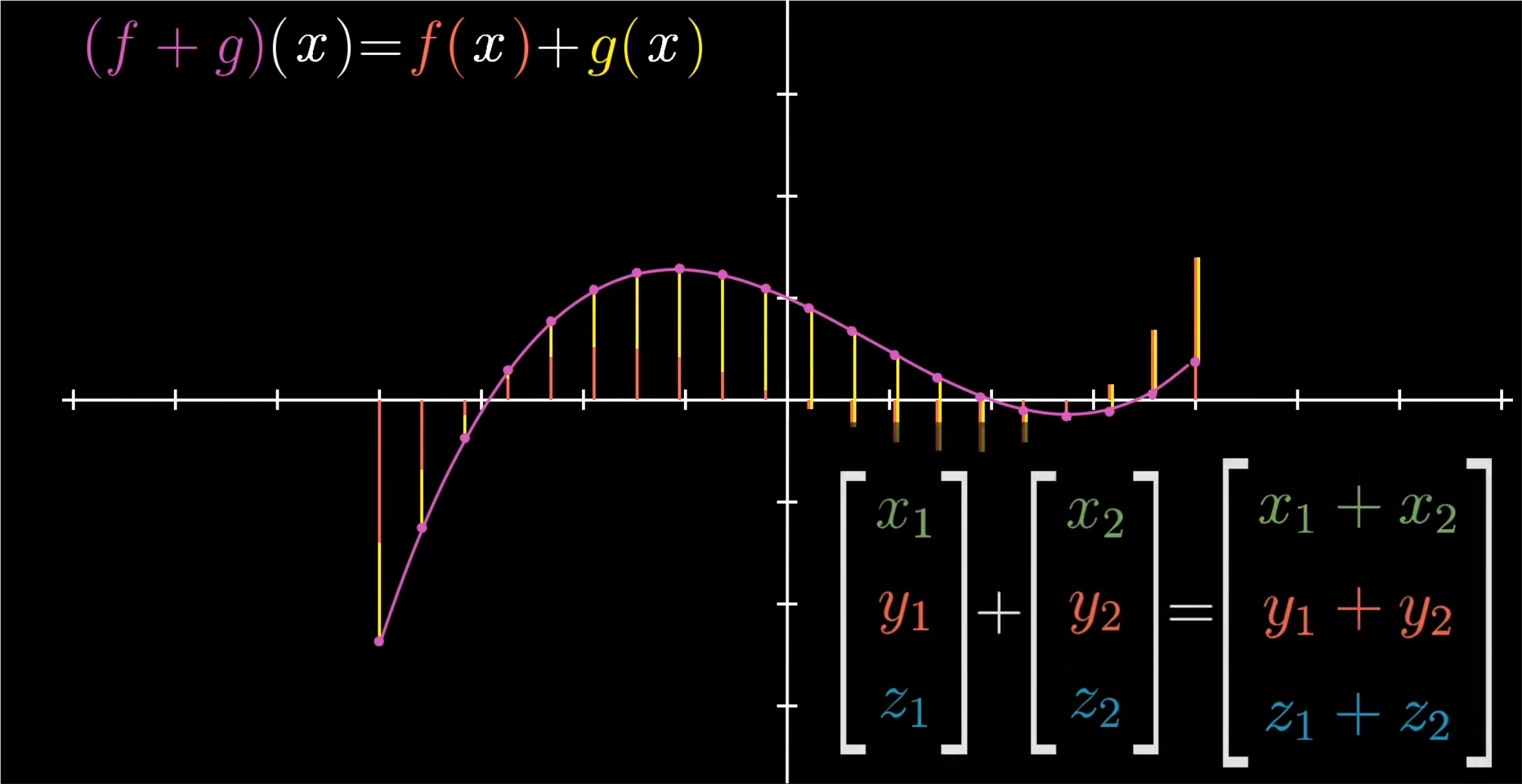
✍️函数与实数:
- 类似的,函数与一个实属相乘也有着合理的解释:
- 我们只是把输出的值与那个数相乘。如下图所示
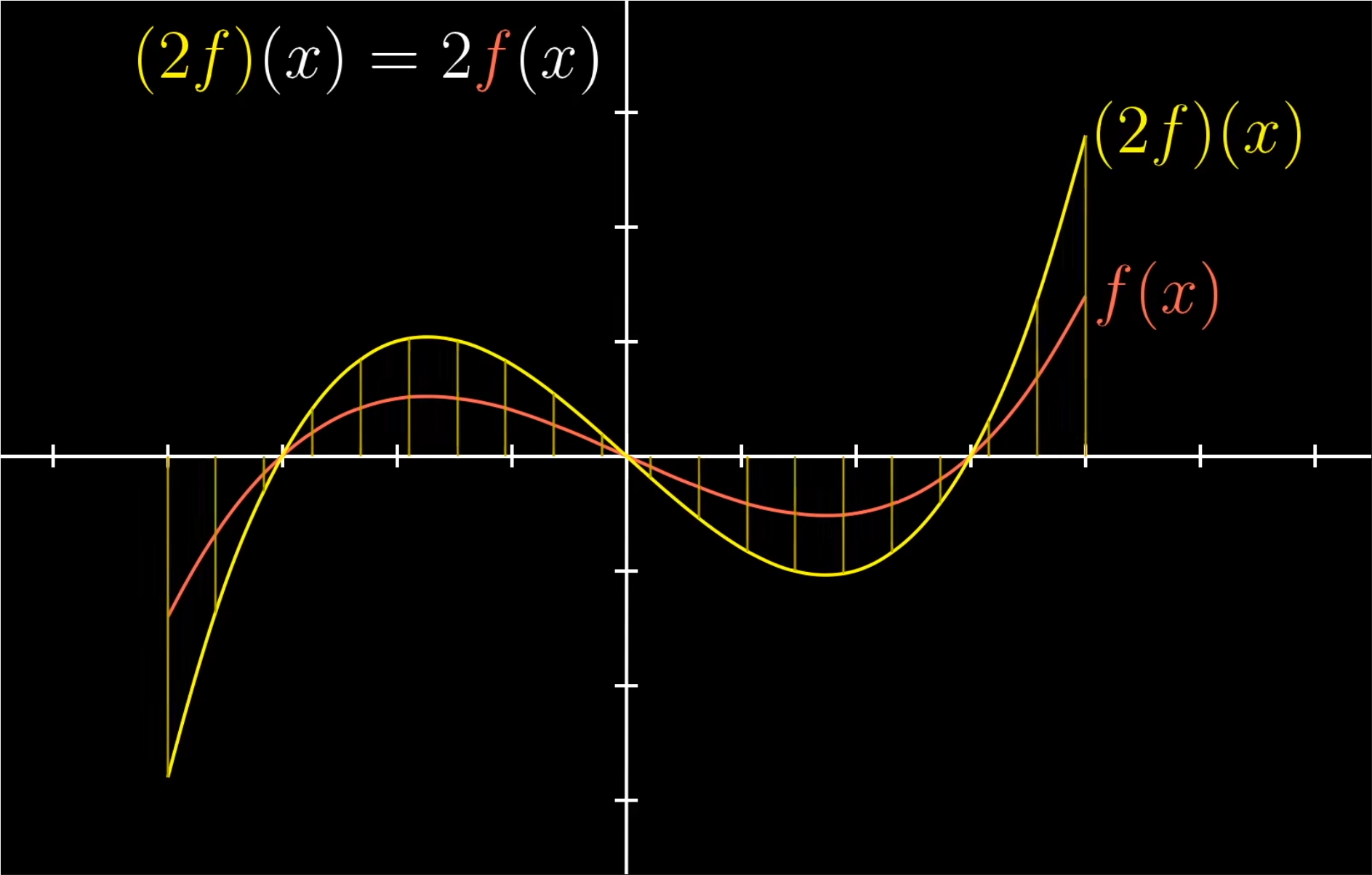
- 这再次和向量对应坐标数乘类似。如下图所示

✍️应用向量的特征到函数:
- 因为对向量所能进行的操作不过向量相加和数乘两种,所以,最初以空间中的箭头为背景考虑的线性代数的合理概念和解决问题的手段,应该能原封不动地被我们取出来,然后应用于函数。
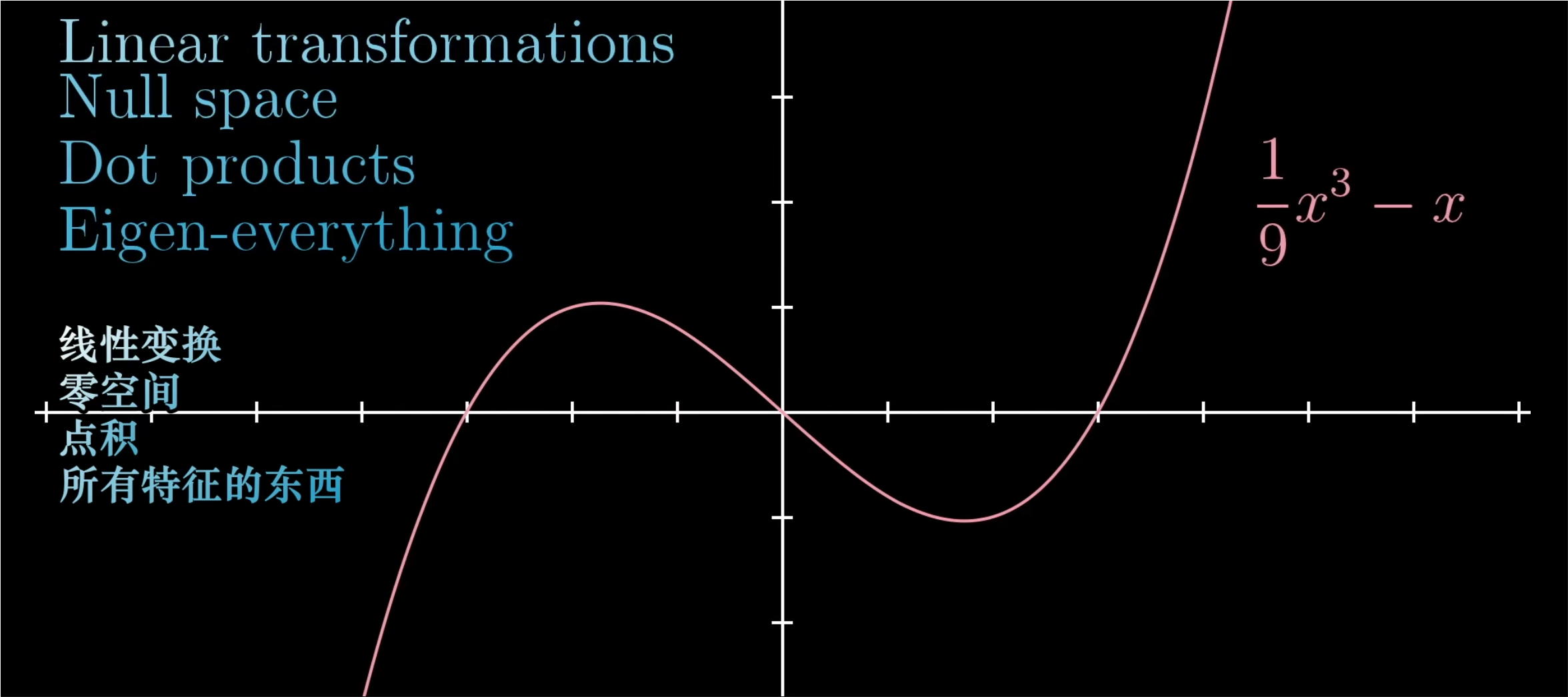
- 举个例子, 函数到线性变换有一个完全合理的解释,这个变换接受一个函数,并把它变成另一个函数;从微积分中可以找到一个常见的例子————导数。他将一个函数变换到另一个函数。
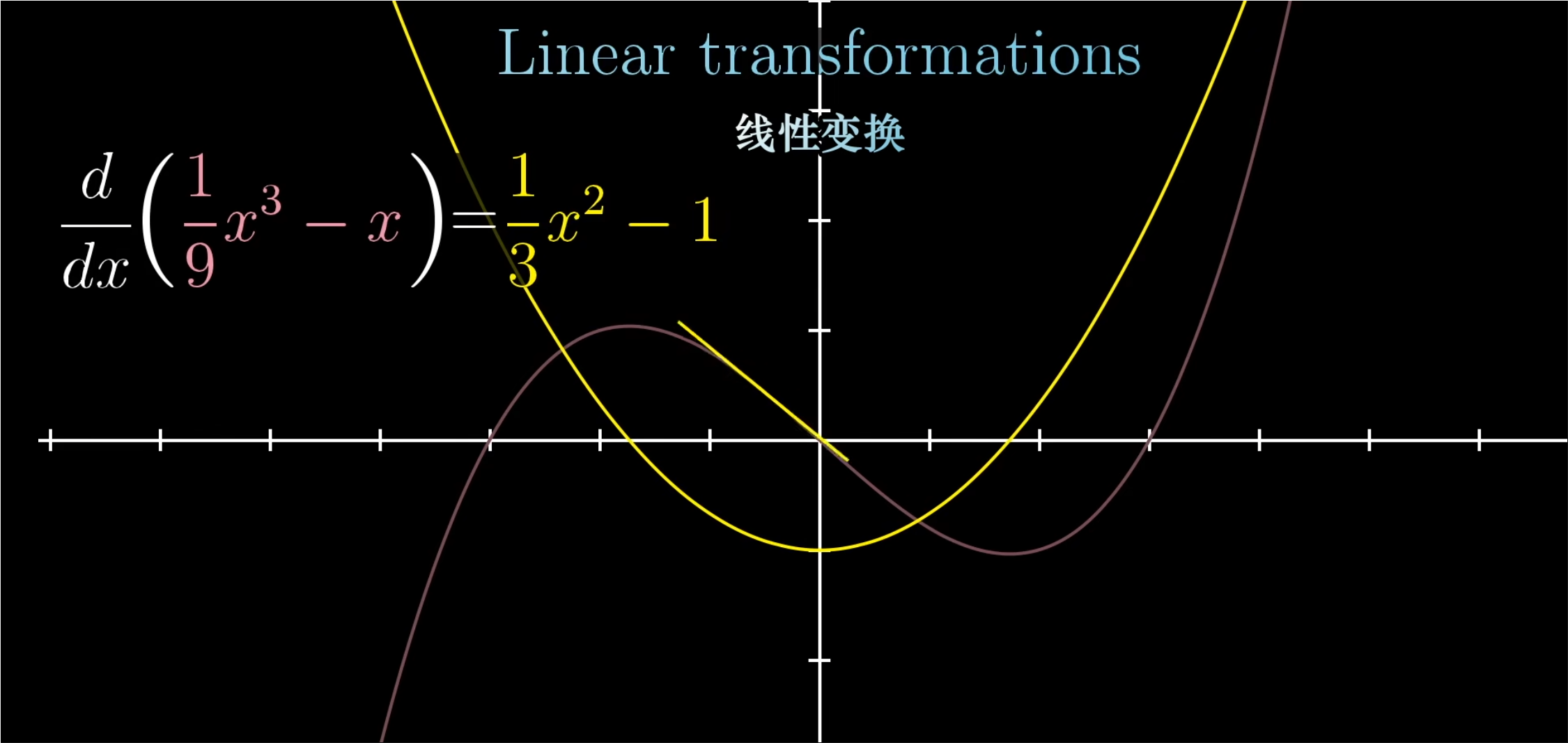
- 有时你听到的是“算子”(线性算子,“Linear operator”)而不是“变换”,它们是一样的。
✍️“一个函数变换是线性的”是什么意思?
- 线性的严格定义是相对抽象而且符号繁重的;但是,抽象性带来的好处是我们能得到一般性的结论,它不仅适用于箭头,也适用于函数。
- 满足以下两条性质的变换是线性的:
- 可加性(Additivity)
- 可加性意味着如果你把两个向量v和w相加,然后对它们的和应用变换,得到的结果和将变换后的v与变换后的w相加一致。
- 成比例(一阶齐次)(Scaling)
- 成比例是说,你讲一个向量v与某个数相乘,然后应用变换,得到的结果和变化后的v与这个数相乘一致。
- 可加性(Additivity)
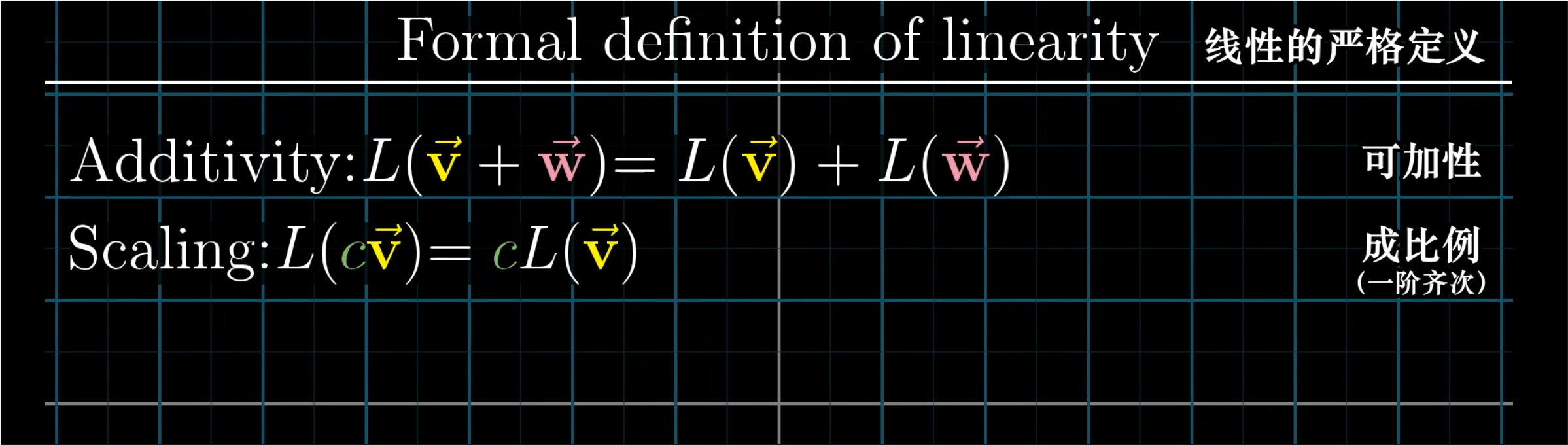
- 你经常会听到一种描述方法是:“线性变换保持向量加法运算和数乘运算”
- 这两条性质的一个最重要的推论就是:一个线性变换可以通过它对基向量的作用来完全描述,这使得矩阵向量乘法成为可能。因为任一向量都能表达为基向量以某种方式进行的线性组合,所以求一个向量变换后的结果,实际上就是求出变换后的基向量以相同方式进行线性组合的结果。
- 这就跟箭头一样,这一点对函数来说同样正确。
求导(Derivative)是线性运算:
- 举个例子:
- 求导(Derivative)是线性运算。
- 如果你把两个函数相加,然后求导数;等同于先求两个函数的导数,然后把结果相加。
- 类似的,如果你将函数与数相乘,然后求导数;等同先求导数,然后把结果相乘。


✏️用矩阵来描述求导:
这可能有些棘手,因为函数空间倾向于有无穷维。
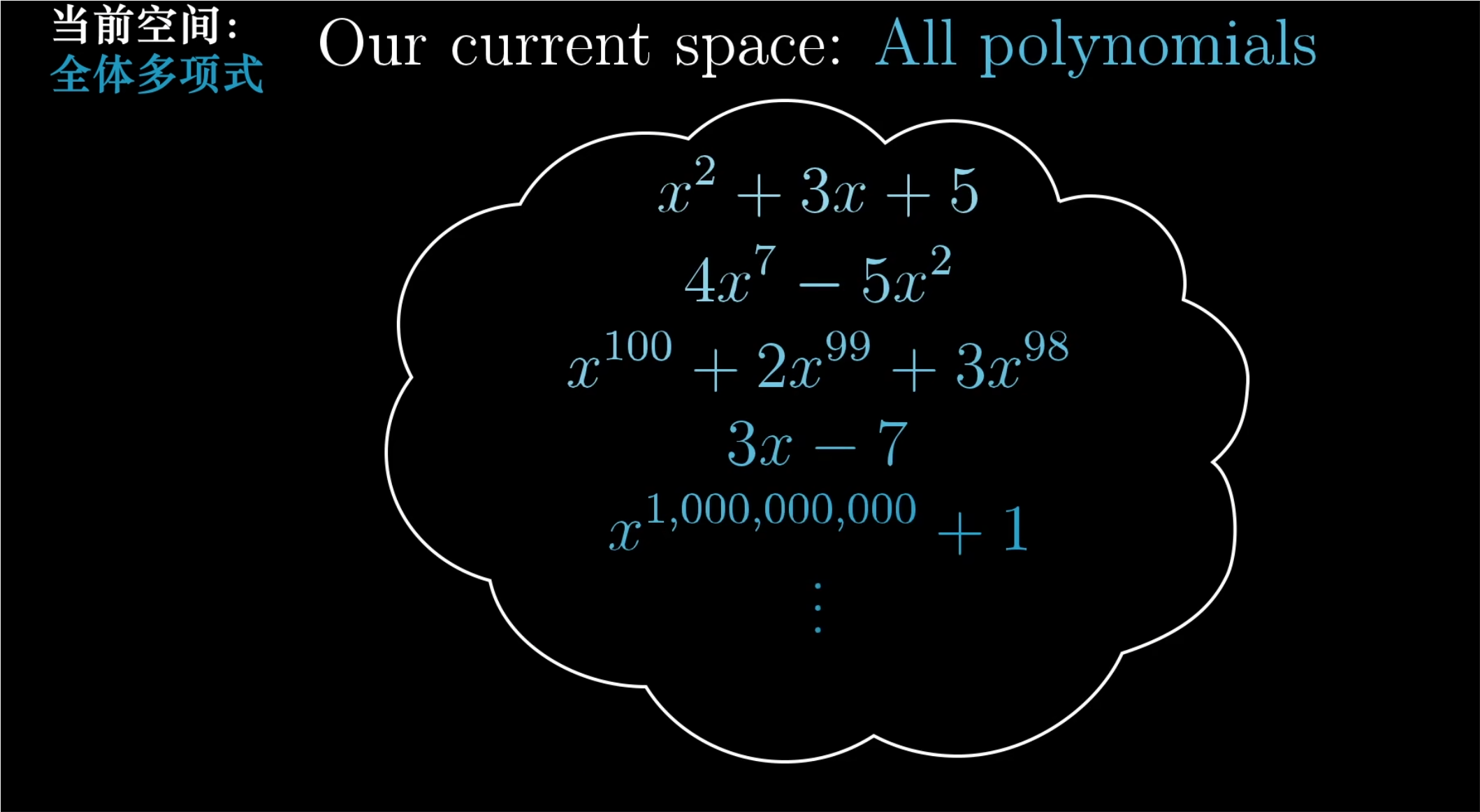
- 我们现在把目光限制在多项式空间上,如上图,有几个多项式。虽然这个空间中每一个多项式都只有有限项,但整个空间应该包含任意高次的多项式。
- 首先我们要做的是给这个空间赋予坐标的含义,这需要选取一个基。
- 因为多项式已经是数乘x的不同次幂再做加和的形式,所以我们很自然就可以去x的不同次幂作为基函数(basis function)。换句话说,第一个基函数就是一个常函数,即b0(x)=1;第二个基函数是b1(x)=x;第三个基函数是b2(x)=x^2;依此类推。
- 基函数在这里起到的作用,和i帽,j帽,k帽在向量的世界中起到的作用类似。
- 因为多项式的次数可以任意高,所以这个基函数集也是无穷大的。
- 如下图,取出多项式的坐标,然后把它放在矩阵的右侧。对结果的第一个坐标有贡献的只有1乘以4这一项,也就是说结果的常数项是4。这对应用于4x的导数是常数4.
- 对矩阵向量乘积的第二个坐标有贡献的只有2乘以5这一项,也就是说结果中x前的系数是10。
- 与之相似的,矩阵向量乘积的第三个坐标就是3乘以1,这对应于x^3 的导数是 3x^2。
- 在此之后的坐标都是0。
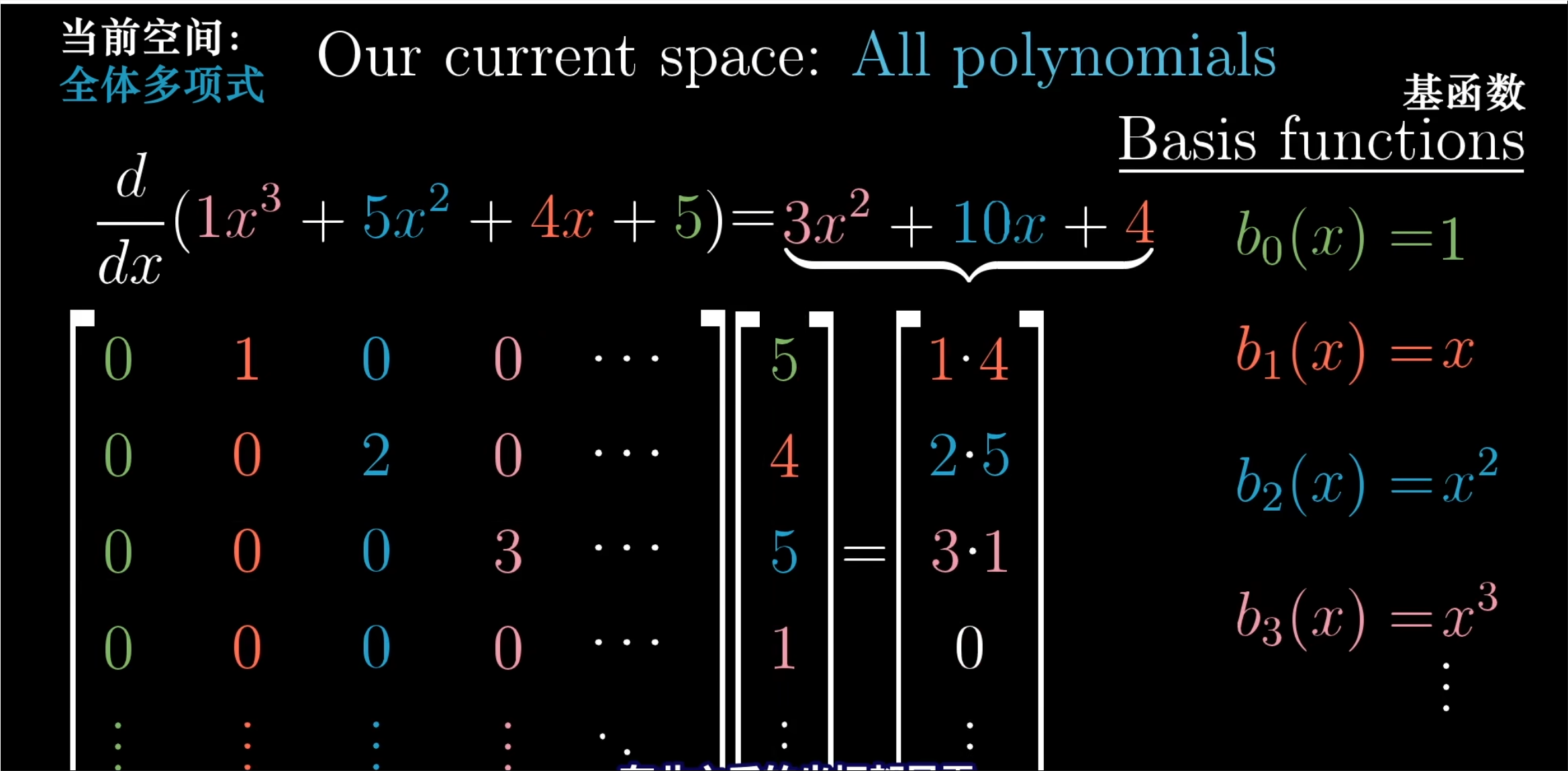
- 求导满足线性性质是这一过程成为可能。
✍️线代和函数中概念之间的关联
- 矩阵向量乘法看起来好像跟求导毫不相干,但是它们其实是一家人。我们提到的许多线性代数的概念,在函数中都能找到对应的别名。

✏️公理(Axioms):
✍️上述提到的与向量有什么关系?:
- 数学中有很多类似向量的事物,只要你处理的对象集具有合理的数乘和相加的概念,不管是空间中的箭头,一组数,函数的集合,还是自定义的其他奇怪东西的集合;线性代数中所有关于向量,线性变换和其他概念都应该适用于它。
- 这些类似向量的事物,它们构成的集合被称为“向量空间”。
- 为了这些构想出来的向量空间合理,我们需要做的是建立一系列向量加法和数乘必须遵守的规则,如下:
- 向量加法满足结合律
- 向量加法满足交换律
- 向量加法的单位元存在
- 每个向量的加法逆元均存在
- 标量乘法与标量的域乘法相容
- 标量乘法的单位元纯真
- 标量乘法对向量加法满足分配律
- 标量乘法对域加法满足分配律

- 如上所述,这些规则被称为“公理”(Axioms)。
- 在线性代数的现代理论中,如果要让所有已经建立好的理论和概念适用于一个向量空间,那么它必须满足上述的八条公理。
- 不过这些实际上就是一个清单,用来保证向量加法和数乘的概念确实是你所希望的那样。
✍️公理的作用:
- 这些公理并非基础的自然法则,它们是一个媒介(interface);也就是发现这些结论的数学家一边连接着你,一边也连接着其他的人,也就是想要把这些结论应用于新的向量空间的人。
- 有了这些公理,我们只需要根据这些公理去证明你的结论就可以了。只要其他人的定义满足这些公理,他们就能顺利的应用你的结论。
- 因此,你往往会把你所有的结论抽象的表述出来;也就是说仅仅根据这些公理表述,而不是集中于某一种特定的向量上,像是空间中的箭头或者函数等。
- 简而言之,这就是每一本教科书都会根据可加性和成比例性来定义线性变换,而不是用我们之前看到的“网格线保持平行且等距分布来”来定义。
- 所以,只要遵守上述“公理”的东西,都可以被定义为向量。
完结撒花!
《线代本质》的内容这一章其实就是完结啦!!!下一章是《克莱姆法则,几何解释》,由于官方账号发在一起了,所以我会把下一章一起当作这个系列的笔记写在一起,所以下一章是第十二章!
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 ZeTiiCannotStop!
评论






