3Blue1Brown_线代本质第十二章：克莱姆法则，几何解释

• 我开始了3蓝1棕的线性代数本质的学习，我没什么基础所以在此做了笔记，这里是第十二章打卡，学习永远不怕晚哈！如有问题请各位大佬及时指正！
• 《线代本质》的内容在我的第十一章的笔记就是完结篇，这篇第十二章《克莱姆法则，几何解释》由于官方账号发在一起了，所以我也当作这个系列一起写了
• 在b站它的链接在此。
• 官方一共将此系列分为12节，所以我也会分开写。
• 我会把相关的这一系列笔记链接在每一篇的最下面，写完就会更新，有需要的朋友可以自行跳转！
• 这就是普通的记录，比较基础，没什么有新意的地方。厉害的大佬或相关专业的大佬可以自行跳过此笔记！

---

✏️克莱姆法则，几何解释：

✍️克莱姆法则以及背后的几何原理：

• 克莱姆法则是线性代数中一个关于求解线性方程组的定理。它适用于变量和方程数目相等的线性方程组。
• 克莱姆法则并不是计算线性方程组最好的方法，比如高斯消元法（Gaussian Elimination）会算的更快。这一部分内容就可以当作是扩展视野，它会帮你加深对线性方程组的理解。
• 在知道了这方面的知识后，你就会发现行列式或者线性方程组，这些知识都非常相关。
• 举例来说：这里有x和y两个未知数和两个方程，原则上来说，只要未知数和方程个数一样，我们所说的都适用。
• 目前，我们将只讨论非零行列式的情况。这意味着线性变换后不改变维数。每个输入向量有且仅有一个输出向量；且每一个输出向量也仅对应一个输入向量。

---

✍️正交变换（Orthonormal）：

• 那些不改变点积的矩阵变换有一个特殊的名字：“正交变换”（Orthonormal）。它们使基向量在变化后依然保持单位长度且互相垂直。
• 可以想象成是旋转矩阵，相当于刚体运动，没有拉伸，压缩或者变形。
• 用正交矩阵来求解线性系统非常简单，因为点积保持不变，所以已知的输出向量和矩阵的列向量的点积，分别等同于未知输入向量和各个基向量的点积。也就是输入向量的每一个坐标。
• 因此，在特殊情况下，x等于第一列向量已知向量的点积，y等于第二列向量与已知向量的点积。
  
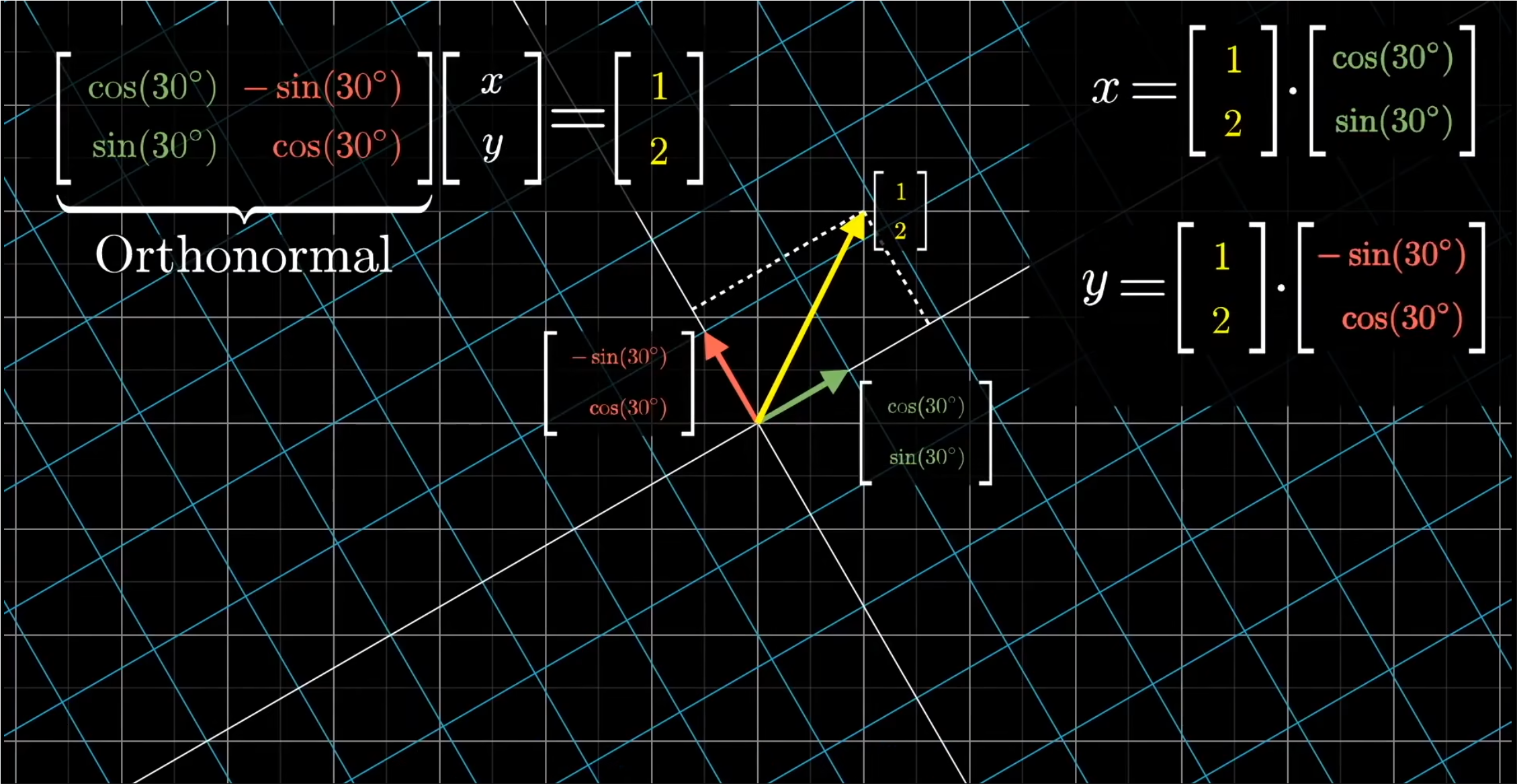
• 注意：这个思路对于大多数线性方程组都不成立，但是他给了我们一个方向去思考：有没有另一种对输入向量坐标值的几何解释，能在矩阵变换后保持不变呢？

---

在二维空间中：

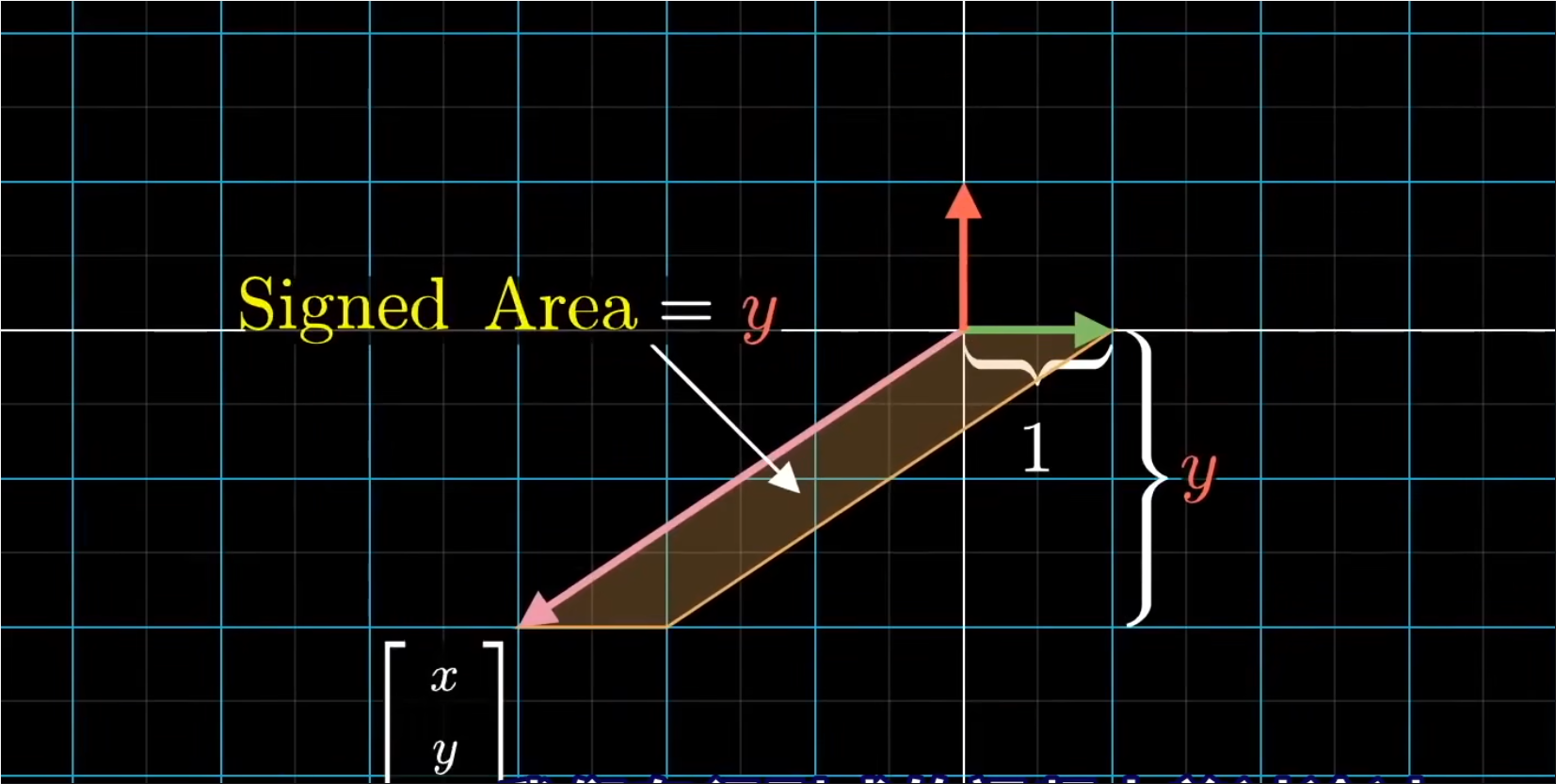
• 如果逆非常熟悉行列式，你可能会想到一个很棒的想法：这个由第一个基向量i和位置的输入向量[x；y]组成的平行四边形；面积是长度为1的底，乘上与底边垂直的高（也就是输入向量y的坐标值）。
• 因此，我们拐了一个弯，用这个平行四边形的面积来表示y值。
• 更准确的说，你应该考虑这个平行四边形的有向面积。如下图所示。
• 正如行列式的那样，如果向量y的坐标为负，那么四边形的面积也为负。前提是你把基向量i放在第一位来定义平行四边形。
  
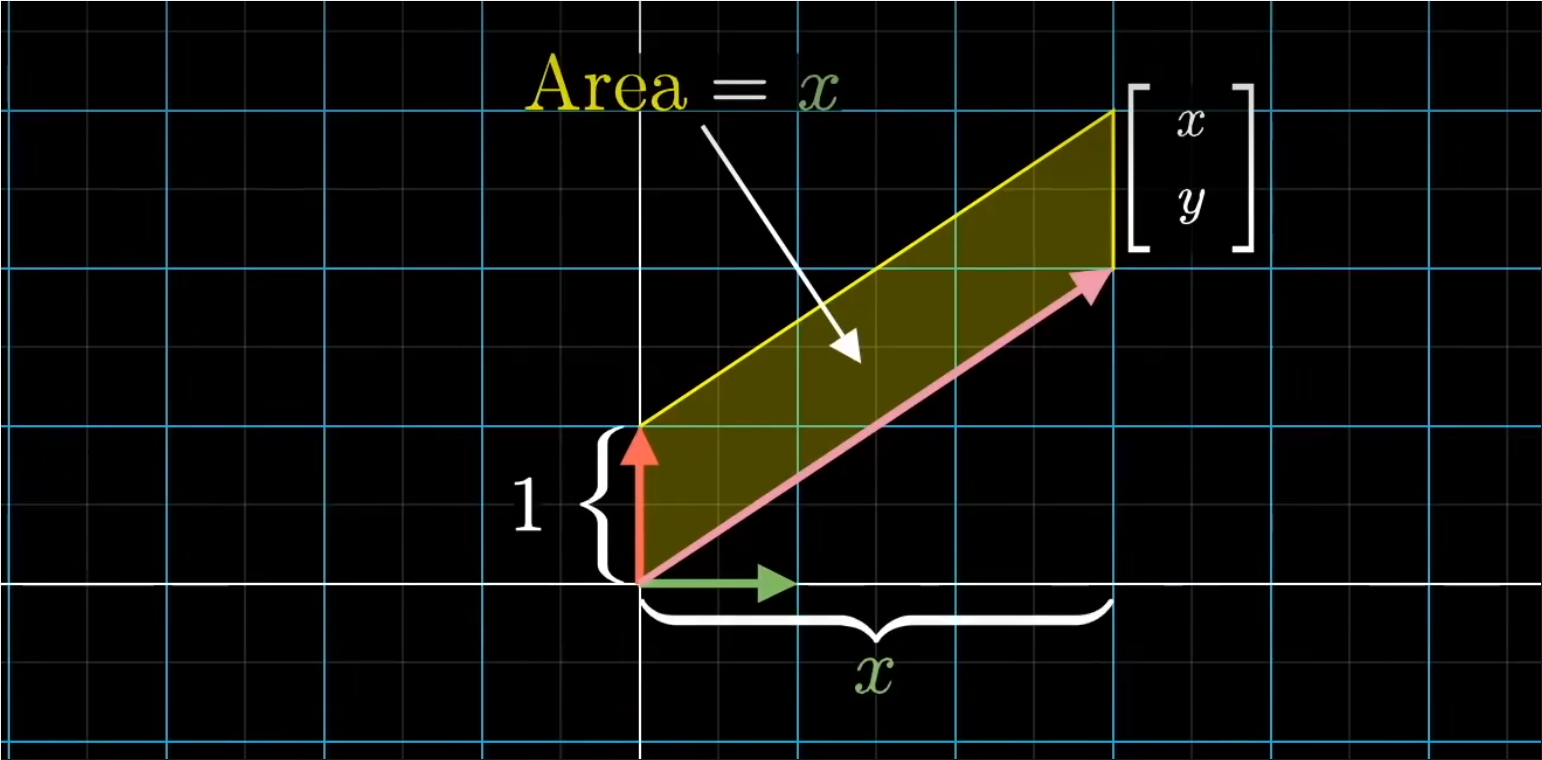
• 同样，观察由未知的输入向量和第二基向量j组成的平行四边形；它的面积等于向量的x坐标。
• 用这种方式表示x的值也有点奇怪。
  

---

在三维空间中：

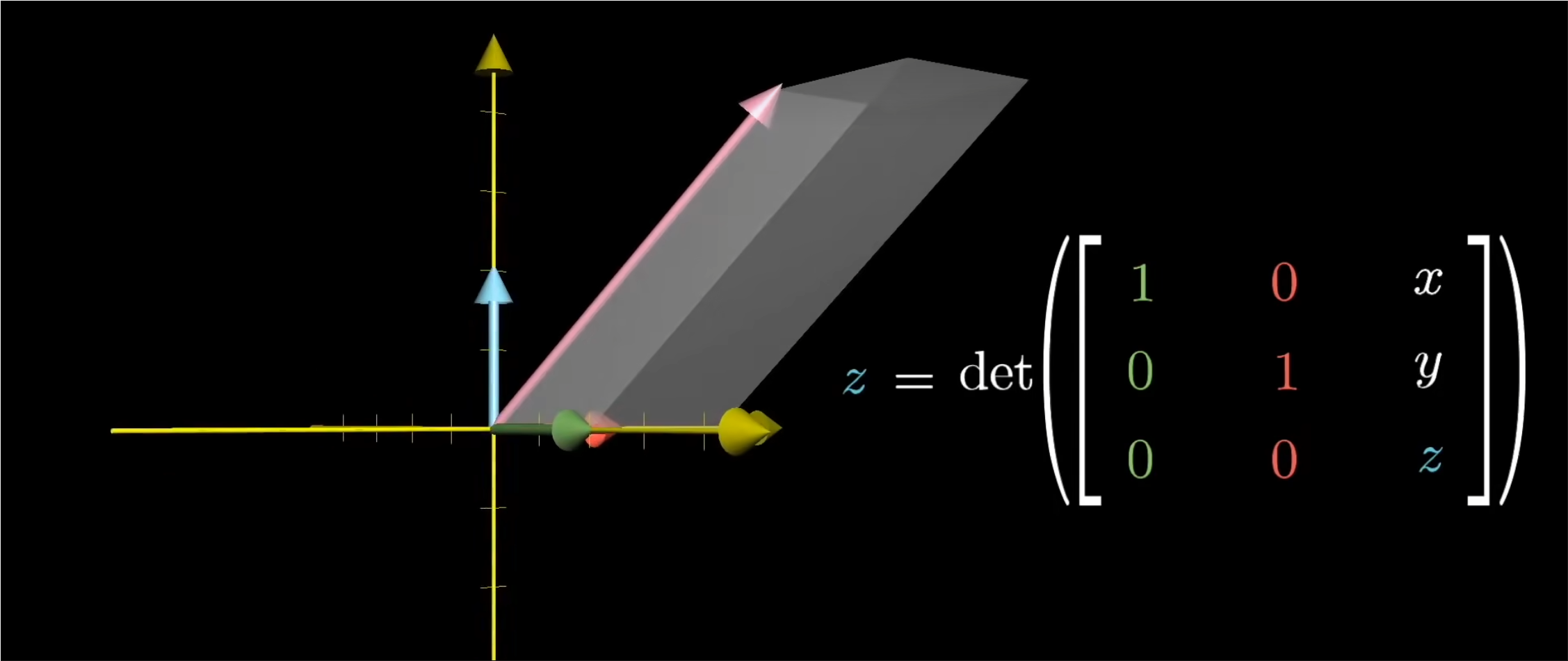
• 考虑向量与另外两个基向量i和j所组成的平行六面体，底面是由基向量i和j组成的正方形，面积是1；所以他的体积等于它的高，也就是我们这个向量的z坐标。
• 同样的，用这个奇怪的方法来描述向量在某一个轴上的坐标值，可以先考虑向量，和除了这个轴紫外的两个基向量组成的平行六面体。然后其体积就是对应的坐标值。
• 另外，我们可以讨论平行六面体的有向体积，就是之前在行列式中提到过的右手法则。这时，你列出的这三个向量的顺序就很重要了。这样就表明坐标的正负性也是有意义的。

---

✍️将坐标值和面积或体积联系起来的意义：

• 因为当你做矩阵变换后，平行四边形的面积不一定保持不变，可能成比例的增大或减小。但是，所有面积伸缩的比例都是一样的，都等于给定变换矩阵的行列式。
  
• 考虑一个新的平行四边形；第一条边是变换后的第一基向量（也就是矩阵的第一列）；第二条边是变换后的[x,y]，那它的面积是多大呢？
• 其实这就是我们之前提及的平行四边形的变换。变换前，面积是未知输入向量的y坐标值，所以变换后的面积等于矩阵的行列式乘以y值。
• 所以可以用输出的平行四边形面积除以矩阵的行列式计算出y。既然我们已知最终变换后的向量，那么可以构造一个新矩阵，第一列和我们原先的矩阵相同，而第二列是输出向量，然后取新矩阵的行列式。如下图所示。
  
• 我们只需使用到变换后的两个向量，也就是矩阵的列向量和已知输出向量，就能计算出位置输入向量的y值，此时方程已经解好一半了。
• 我们可以用相同的方法得出x值。如下图所示。
  
• 这个线性方程组的解法，被称为克莱姆法则。
• 三维或者多维的计算结果也基本如此。

---